摘要： 螺栓球节点常用于网架及双层网壳结构中，目前在一些小跨度、接近球形的单层网壳中也有所应用。现阶段对螺栓球节点网架及双层网壳进行分析时，通常将螺栓球节点假定为理想铰接，实际上该节点是介于刚接和铰接之间的半刚性节点。通过建立螺栓球节点的精细化模型，得到螺栓球节点的抗弯刚度及对应的弯矩-转角曲线，并利用已有试验数据验证了数值模型的合理性。研究了螺栓球节点相关参数（即螺栓直径、预紧力大小、锥尾壁厚和套筒厚度）对节点抗弯刚度的影响。研究表明：螺栓球节点的初始刚度和极限弯矩在一定范围内随螺栓预紧力的增大而提高，当螺栓预紧力达到100kN时，其对螺栓球节点抗弯刚度的影响逐渐减弱；锥尾壁厚及套筒厚度对螺栓球节点极限弯矩的影响较大，而对节点初始刚度的影响较小；螺栓球节点的抗弯刚度随着螺栓直径的增加而增大。利用对螺栓球节点参数化分析的结果并结合节点的自身特性，基于KISHI等提出的幂函数模型，推导出了螺栓球节点弯矩-转角关系公式，该公式计算值与数值模拟的弯矩-转角曲线吻合度较高，能有效地模拟螺栓球节点弯矩-转角的关系。

关键词： 螺栓球节点；弯矩-转角曲线；抗弯刚度；弯矩-转角关系式；参数化分析

Abstract： Bolt-ball joints are commonly used in grid structures and double-layer reticulated shells and are also extended to some small-span， approximately spherical reticulated shells. When analyzing the grid structures and double-layer reticulated shells with bolt-ball joints， the bolt-ball joint is usually assumed to be an ideal articulated joint. The joint is a semi-rigid joint between a rigid and articulated joint. In this paper， by establishing a refined model of the bolt-ball joint， the bending stiffness and the corresponding moment-rotation curve of the bolt-ball joint are obtained， and the experimental data verify the rationality of the numerical model；the effects of relevant parameters of the bolt-ball joint （e.g.， bolt diameter， pre-tightening force， cone tail wall thickness， and sleeve thickness） on the bend-bearing capacity of the bolt-ball joint are explored. The results of the research show that the initial stiffness and ultimate bending moment of the bolt-ball joint increase with the increase of pre-tightening force applied by the bolt in a specific range. When the bolt pre-tightening force reaches 100kN， its influence on the bend-bearing capacity of the bolt-ball joint gradually weakens；The thickness of the cone tail and sleeve has a more significant influence on the ultimate bending moment of the bolt-ball joint but has a minor influence on the initial stiffness of the joint；the bend-bearing capacity of the bolt-ball joint increases with the increase of the bolt diameter. Based on the results of parametric analysis of the bolt-ball joint and combined with the characteristics of the joint， the power function model proposed by KISHI and CHEN is used to deduce the moment-rotation relation formula of the bolt-ball joint. The calculated value of this formula is in good agreement with the moment-rotation curve of the numerical simulation and can effectively simulate the moment-rotation relationship of the bolt-ball joint.

Keywords： bolt-ball joint；moment-rotation curve；bending stiffness；moment-rotation relation formula；parametric analysis

网壳结构是大跨度空间结构中的一种常见形式，广泛应用在航站楼、体育馆、展览馆和会展中心等大型公共建筑中。节点作为网壳重要组成部件之一，其力学性能会影响网壳结构的整体受力性能。我国《空间网格结构技术规程》（JGJ 7—2010） ^[1] 建议将螺栓球节点假定为铰接节点，忽略其抗弯刚度，建议用在网架及双层网壳结构中。实际上，螺栓球节点具有一定的抗弯能力，是介于刚接与铰接之间的一种半刚性节点 ^[2] ，这种半刚性节点具有一定的抗弯承载力，受力性能不同于理想的刚接或铰接节点。

目前，国内外学者对半刚性节点及半刚性节点网壳结构在受力性能和稳定性等方面展开了大量的研究。陈耕博 ^[3] 对Scoket节点进行试验与有限元分析，研究结果表明Scoket节点的抗弯能力随螺栓直径、外垫片直径和压弯应力比的增加而提高，根据参数分析结果提出了符合该节点有限元模型的弯矩-转角关系公式；尹晨光 ^[4] 通过对现有半刚性节点的不同形式及研究现状进行总结，提出了一种新型复式球节点，并对新型复式球节点进行试验与数值模拟分析，通过观察试验中节点的破坏形态和分析数值模拟所得结果中的相关数据，与传统焊接球节点的承载力进行对比，得出新型复式球节点的承载能力可达到传统焊接球节点的承载能力，并计算出该新型复式球节点的弯矩-转角关系公式；廖俊等 ^[5] 对焊接空心球节点建立有限元模型，并对大量有限元模型进行分析，发现该节点的荷载-位移曲线符合双线性模型。基于此，确定了屈服系数和刚度系数的取值，拟合出焊接空心球节点初始刚度和极限弯矩的三次多项式公式，最终确立出焊接空心球节点的荷载-位移双线性模型；ERLING ^[6] 研究了螺栓球节点的转动能力和节点抗弯刚度对球面网壳极限承载力的影响；KATO等 ^[7] 、SOHN等 ^[8] 研究了节点刚度对空间结构极限承载力的影响；范峰等 ^[9] 、马会环 ^[10] 对螺栓球节点单层球面网壳进行了稳定性分析，研究表明节点的弯曲刚度和荷载分布形式是影响单层球面网壳结构稳定性的重要因素，节点的扭转刚度对网壳结构的稳定性无显著影响；薛素铎等 ^[11] 提出了一种在节点域用梁单元代替空心球节点建立网壳结构的简化模型，可通过减小节点域的杆件刚度，使简化模型与精细化模型的分析结果接近，表明该简化模型更适用于单层柱面网壳结构在强震作用下的失稳分析。

本文采用数值方法对螺栓球节点进行精细化建模及分析，得到螺栓球节点的弯矩-转角曲线，并研究螺栓球节点相关参数对弯矩-转角曲线中各项特征参数（初始刚度、初始屈服弯矩、塑性屈服刚度和极限弯矩）的影响，推导出螺栓球节点弯矩-转角关系公式。

1　螺栓球节点数值模型研究

1.1　建模及加载方式

螺栓球节点由螺栓球、套筒、锥头和高强度螺栓等构件组成。本文在ANSYS中选用Solid45实体单元模拟螺栓各部分构件，由于螺栓球节点各构件之间的相互作用是通过接触面实现，故采用模拟接触法 ^[12] 对螺栓球节点进行实体建模，即在ANSYS中采用Conta174与Targe170接触单元模拟各构件之间的接触面。接触面设置如图1所示。

节点球的上半部分全部约束，在锥头端部的中心处建立一个节点，使中心节点与锥头底面的其他受力节点分别形成多根刚性梁，将图2所示方向的弯矩荷载施加在中心节点上，弯矩荷载通过刚性梁传递。

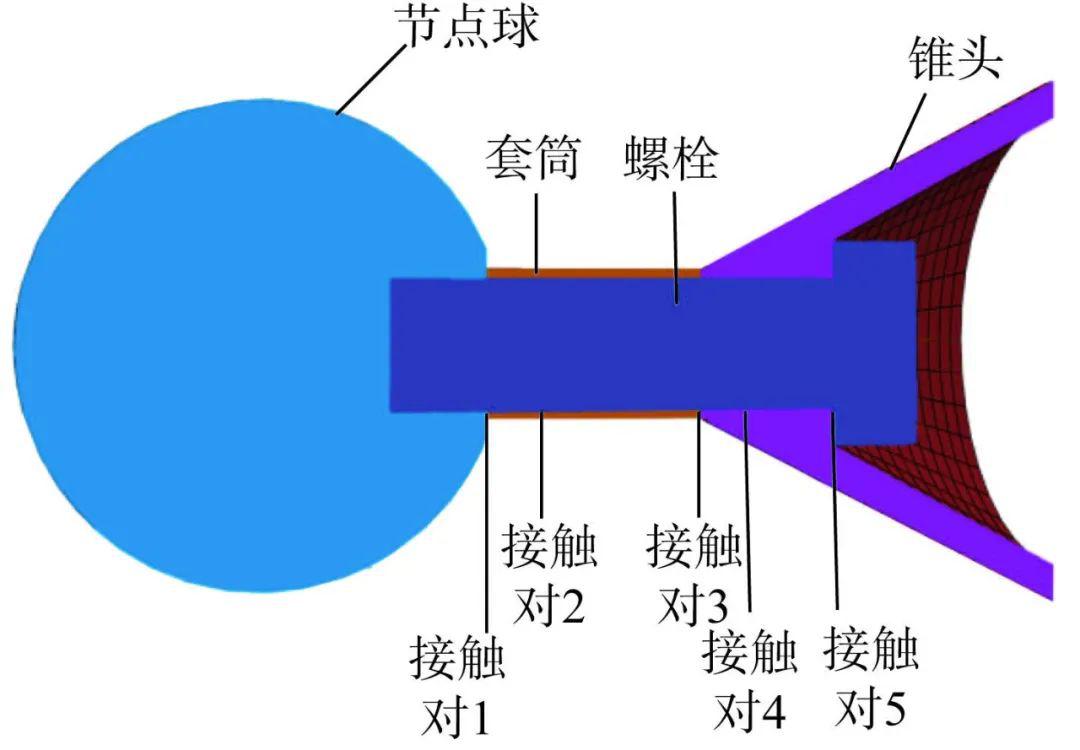
图1　螺栓球节点构造及接触对

Fig.1　Details and contact pairs of bolt-ball joint

图2　弯矩施加方向

Fig.2　Direction of moment application

1.2　模型验证

为验证本文所建数值模型的可靠性，参考范峰等 ^[13] 试验中试件的尺寸、材料特性和加载方式，进行有限元建模及加载。螺栓球直径为100mm，螺栓杆直径为27mm，套筒、锥头和钢管的尺寸与螺栓配套且强度均为235MPa，螺栓球采用45 ^# 钢，强度为365MPa，高强度螺栓采用40Cr钢，强度为430MPa，预紧力为20kN。节点位移云图及螺栓的应力状态如图3所示。可以看出：当螺栓球节点承受如图2所示方向的纯弯矩荷载作用时，套筒与螺栓球接触面、套筒与锥头接触面的上部紧靠，下部基本呈脱离状态，螺栓杆产生向上的弯曲变形，这与螺栓球节点的实际工作状态相符。

图3　模拟结果

Fig.3　Simulation results

将数值模拟与试验 ^[13] 获得的弯矩-转角曲线进行对比，结果如图4所示。可以看出：数值模拟与试验的弯矩-转角曲线在塑性阶段吻合较好，极限弯矩值基本相同；二者的弯矩-转角曲线在弹性阶段产生微小偏差，数值模型的初始刚度较试验模型的初始刚度稍大，该误差产生的原因可能是高强度螺栓的材料性能与实际情况存在偏差或施工误差等因素引起的。从数值模拟与试验弯矩-转角曲线的总体发展趋势和拟合程度来看，本文采用的螺栓球节点数值模拟方法能较好地模拟螺栓球节点真实的受力情况。

图4　数值模拟与试验的弯矩-转角曲线

Fig.4　The moment-rotation curves of numerical simulation and test

2　节点参数化分析

2.1　螺栓预紧力对节点弯曲刚度的影响

对螺栓球节点而言，螺栓预紧力大小对螺栓球节点抗弯刚度的影响很大，设计螺栓球节点时应该考虑预紧力大小对其受力性能的影响。因此，本节对螺栓分别施加大小为20kN、50kN、70kN、80kN、90kN、100kN、120kN和200kN的预紧力，对上述不同预紧力作用下的螺栓球节点进行参数分析，分别得到在不同螺栓预紧力作用下螺栓球节点的弯矩-转角曲线，如图5所示。螺栓球节点的其他参数设置如下：螺栓直径为27mm，锥头尺寸为20mm×5mm（锥头底板厚为20mm，锥尾壁厚为5mm），套筒尺寸为27mm×45mm×40mm（套筒内径为27mm，外径为45mm，长度为40mm）。本文螺栓球节点的材料选用如下：10.9级高强度螺栓，屈服强度为940MPa，螺栓球采用45 ^# 钢，屈服强度为365MPa，锥头和套筒采用Q235钢，屈服强度为235MPa。

如图5所示，螺栓预紧力在一定范围内会对螺栓球节点的抗弯刚度产生较大影响，当螺栓预紧力小于100kN时，弯矩-转角曲线中的初始刚度和极限弯矩值随着预紧力增加而增大；当螺栓预紧力为100kN时，螺栓球节点的初始刚度与极限弯矩显著增大；当螺栓预紧力大于100kN时，随着预紧力继续增加，螺栓球节点的初始刚度和极限弯矩变化并不显著，此时螺栓预紧力对节点抗弯刚度的影响逐渐减弱。因此，当螺栓预紧力为100kN时，达到螺栓球节点抗转动能力的界值，该模型的临界预紧力为100kN。

图5　不同预紧力作用下的弯矩-转角曲线

Fig.5　Moment-rotation curves under different preloads

2.2　锥尾壁厚对节点弯曲刚度的影响

螺栓球节点的锥头部分（图6）受力复杂，应力分布不均匀，对螺栓球节点的抗弯能力有所影响。因此，对不同锥尾壁厚的螺栓球节点进行参数分析，分别建立锥尾壁厚为3mm、5mm、8mm和11mm的数值模型并得到其弯矩-转角曲线（图7）。节点的其他参数设置为：螺栓直径为24mm，套筒尺寸为24mm×39mm×40mm（套筒内径为24mm，外径为39mm，长度为40mm），预紧力为20kN。

图6　锥头构造

Fig.6　Construction of the cone

由图7中节点初始刚度和极限弯矩随锥尾壁厚变化的规律可以看出：锥尾壁厚对螺栓球节点极限弯矩的影响显著。增加锥尾壁厚能在一定范围内提高螺栓球节点的抗转动能力，但由于锥尾壁厚对节点初始刚度的影响并不显著且壁厚增加导致结构自重增大，因此对螺栓球节点进行设计时，锥尾壁厚不宜过厚。

图7　不同锥尾壁厚下的弯矩-转角曲线

Fig.7　Moment-rotation curves with different cone tail thickness

2.3　螺栓直径对节点弯曲刚度的影响

由文献[14]可知，螺栓直径对螺栓球节点的初始刚度和极限弯矩等其他特征参数有显著的影响。因此本节对螺栓直径分别为24mm、27mm和30mm的螺栓球节点进行分析。螺栓球节点随螺栓直径变化的弯矩-转角曲线如图8所示。节点的其他参数设置如下：螺栓直径为24mm的螺栓球节点，对应的锥头底板厚度为16mm；螺栓直径分别为27mm和30mm的螺栓球节点，对应的锥头底板厚度为20mm；套筒尺寸依据《钢网架螺栓球节点用高强度螺栓》（GB/T 16939—2016） ^[15] 设置，预紧力均为20kN。

图8　不同螺栓直径下的弯矩-转角曲线

Fig.8　Moment-rotation curves with different bolt diameters

由图8可得，螺栓球节点的初始刚度、初始屈服弯矩、塑性屈服刚度和极限弯矩均随着螺栓直径的增大而提高。螺栓直径对螺栓球节点抗转动能力的影响非常大，M30螺栓球节点的初始刚度和极限弯矩值明显高于M24与M27的初始刚度和极限弯矩值。各项特征参数的具体变化如表1所示。

可以看出：当螺栓直径为30mm时，其初始刚度值是螺栓直径为24mm的2.18倍；不同螺栓直径下的极限弯矩值也相差很大，当螺栓直径为30mm时，其极限弯矩是螺栓直径为24mm的1.81倍。随着螺栓直径的增大，弯矩-转角曲线中的各项特征参数值均随之增大，说明螺栓球节点的抗转动能力随着螺栓直径增大而显著提高。

2.4　套筒厚度对节点弯曲刚度的影响

螺栓球节点受纯弯矩作用时，套筒和球、套筒和锥头的接触面首先出现缝隙，套筒受挤压变形明显，因此可将套筒视为节点抵抗外载作用的重要传力部件 ^[13] 。本节对套筒厚度D _T 分别为3mm、5mm、7mm和9mm的螺栓球节点进行分析，得到螺栓球节点随套筒厚度变化的弯矩-转角曲线如图9所示。节点的其他参数设置如下：螺栓直径为27mm（节点除套筒厚度外，其余构件尺寸同1.2节中M27螺栓球节点的各项尺寸），预紧力为20kN。

图9　不同套筒厚度下的弯矩-转角曲线

Fig.9　Moment-rotation curves with different sleeve thickness

由图9中各项特征参数的变化规律可以看出：节点的初始刚度随着套筒厚度增加而缓慢提高，套筒厚度主要影响螺栓球节点的塑性屈服刚度和极限弯矩。随着套筒厚度的增加，螺栓球节点的极限弯矩及塑性屈服刚度随之显著增大。因此，适当增加套筒厚度可以提高螺栓球节点的抗转动能力。

3　螺栓球节点的弯矩-转角关系公式

3.1　典型模型

国内外学者为可靠估计半刚性连接的受力性能，提出了很多半刚性节点的弯矩-转角曲线模型，如线性模型 ^[16] 、指数函数模型 ^[17] 、幂函数模型 ^[18] 、多项式模型 ^[19] 和B样条模型 ^[20] 等。其中，幂函数模型主要包括二参数模型、三参数模型和四参数模型。KISHI等 ^[21] 提出了一个三参数幂函数模型，其表达式为：

式中：K _i 为半刚性节点的初始刚度；M _u 为半刚性节点的极限弯矩；n为半刚性节点弯矩-转角曲线的形状参数，用于调整节点弯矩-转角曲线的曲率。

3.2　弯矩-转角关系公式的建立

本节利用前文中对螺栓球节点数值模型参数化分析的结果，参考KISHI等 ^[21] 的幂函数模型，结合螺栓球节点自身受力特性，推导螺栓球节点的弯矩-转角关系公式。

由式（1）可知，半刚性节点的初始刚度和极限弯矩是确定半刚性节点弯矩-转角关系公式的重要参数，二者通过修正节点中螺栓的线刚度和极限弯矩得到 ^[22] ，定义如下：

式中：k _Rp 和k _Mp 分别为螺栓预紧力大小对螺栓球节点初始刚度和极限弯矩的影响系数；k _Rd 和k _Md 分别为套筒厚度对螺栓球节点初始刚度和极限弯矩的影响系数，根据前文中预紧力大小和套筒厚度对螺栓球节点抗弯性能的分析结果进行回归分析确定。E _B 、I _B 、l _B 分别为螺栓的弹性模量、惯性矩和长度；f _uB 、A _B 、D _B 分别为抗拉强度、截面面积和螺栓直径。由式（6）和式（7）分别计算出螺栓直径为24mm、27mm和30mm螺栓球节点的初始刚度和极限弯矩，如表2所示。

3.2.1　螺栓预紧力对螺栓球节点初始刚度和极限弯矩的影响系数

根据2.1节中螺栓预紧力大小对螺栓球节点抗转动能力分析结果，将螺栓球节点弯矩-转角曲线中各项特征参数的变化情况整理在表3中。由前文分析结果可知，当对M27螺栓球节点中螺栓所施加的预紧力超过100kN时，其弯矩-转角曲线中各项特征参数的变化较小，故对M27螺栓球节点而言，其临界预紧力为100kN。由表3可知，预紧力对螺栓球节点初始刚度的影响系数k _Rp 与节点中螺栓预紧力和临界预紧力之比的平方成正相关；预紧力对螺栓球节点极限弯矩的影响系数k _Mp 与螺栓预紧力和临界预紧力之比成正相关。

对式（8）和式（9）进行回归分析，分别得到两式中系数A _Rp 、B _Rp 、C _Mp 和D _Mp 的取值。

图10　不同预紧力下的计算值与拟合值

Fig.10　Calculated and fitting values with different preload

3.2.2　套筒厚度对螺栓球节点初始刚度和极限弯矩的影响系数

根据2.4节中套筒厚度对螺栓球节点抗转动能力分析的结果，将螺栓球节点弯矩-转角曲线中各项特征参数的变化情况整理在表4中。

由表4可知，套筒厚度对螺栓球节点初始刚度的影响系数k _Rd 与套筒惯性矩和螺栓惯性矩之比的平方成正相关；套筒厚度对螺栓球节点极限弯矩的影响系数k _Md 与套筒厚度惯性矩和螺栓惯性矩之比成正相关。表4中惯性矩之比是指套筒对其对称轴的惯性矩与螺栓对其对称轴的惯性矩之比，对于直径为27mm的螺栓，其截面惯性矩为2.61cm ⁴ 。

根据上述分析，利用表4中的结果，对式（12）及式（13）进行回归分析，确定参数A _Rd 、B _Rd 、C _Md 和D _Md 的取值。

图11　不同套筒厚度下的计算值与拟合值

Fig.11　Calculated and fitting values with different sleeve thickness

螺栓球节点弯矩-转角曲线的形状参数为n，由非线性回归分析确定为1.2。整理上述分析的结果，推导出螺栓球节点的弯矩-转角关系公式为：

利用式（18）计算前文中已分析的有限元模型，模型及参数设置如表5所示。将公式计算与有限元模拟的弯矩-转角曲线进行对比，如图12所示。

由图12可知，公式计算与有限元模拟弯矩-转角曲线的数值比较接近，在弹塑性阶段基本吻合，未出现较大偏差，总体趋势一致。从数值拟合程度、弯矩-转角曲线的特征参数值和发展趋势观察，建立的螺栓球节点弯矩-转角关系公式能较好地模拟螺栓球节点的半刚性。

图12　公式计算与有限元模拟的弯矩-转角曲线

Fig.12　Moment-rotation curves of formula calculation and finite element simulation

4　结  论

为了获得螺栓球节点的节点刚度，本文对螺栓球节点进行了精细化建模，获得了螺栓球节点的弯矩-转角曲线，并利用已有试验数据验证了模型的合理性，且深入研究了螺栓球节点相关参数对节点抗弯刚度的影响程度，可以得出以下主要结论：

（1）螺栓球节点的刚度及受力特性与螺栓直径、螺栓预紧力大小、套筒厚度和锥尾壁厚有关。螺栓球节点的抗弯刚度随着预紧力的增加而增大，当预紧力增加至100kN时，其对螺栓球节点初始刚度和极限弯矩的影响减弱，故螺栓球节点的临界预紧力为100kN。螺栓直径对螺栓球节点抗弯刚度的影响非常大，节点的初始刚度、初始屈服弯矩、塑性屈服刚度和极限弯矩均随着螺栓直径的增大而提高。套筒厚度和锥尾壁厚主要影响螺栓球节点的极限弯矩，其随着套筒厚度和锥尾壁厚的增加而增大，二者对节点初始刚度的影响不明显。

（2）通过回归分析确定了预紧力大小和套筒厚度对螺栓球节点初始刚度和极限弯矩的影响系数，拟合出了节点初始刚度的二次多项式公式和极限弯矩的线性公式，基于文献[21]提出的三参数幂函数模型，推导出了螺栓球节点的弯矩-转角关系公式。该公式考虑了螺栓预紧力及套筒厚度的影响，能较好地模拟螺栓球节点的弯矩-转角曲线。

参考文献:

[1]中华人民共和国住房和城乡建设部.空间网格结构技术规程:JGJ 7—2010[S].北京:中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Development of the People's Republic of China.Technical Specification for Space Frame Structures:JGJ 7—2010[S].Beijing:China Architecture & Building Press,2010.(in Chinese)

[2]陈耕博.Socket节点性能及其单层球面网壳稳定性研究[D].哈尔滨:哈尔滨工业大学,2010.CHEN Gengbo.Research on Socket node performance and stability of single layer spherical reticulated shell[D].Harbin: Harbin Institute of Technology,2010.(in Chinese)

[3]郭小农,熊哲,罗永峰.空间网格结构节点刚度研究现状简述[J].结构工程师,2014,30(4):185-195.DOI:10.15935/j.cnki.jggcs.2014.04.064.GUO Xiaonong,XIONG Zhe,LUO Yongfeng.State-of-the-art of research on the joint stiffness of the spatial structures[J].Structural Engineers,2014,30(4):185-195.DOI:10.15935/j.cnki.jggcs.2014.04.064.(in Chinese)

[4]尹晨光.空间钢结构新型复式球节点性能分析与试验研究[D].南京:东南大学,2016.YIN Chenguang.Performance analysis and experimental study of new compound spherical joint in space steel structure[D].Nanjing: Southeast University,2016.(in Chinese)

[5]廖俊,张毅刚.焊接空心球节点荷载-位移曲线双线性模型研究[J].空间结构,2010,16(2):31-38.DOI:10.13849/j.issn.1006-6578.2010.02.005.LIAO Jun,ZHANG Yigang.The study of bilinear model for loading-deformation curve of welded hollow spherical joints[J].Spatial Structures,2010,16(2): 31-38.DOI:10.13849/j.issn.1006-6578.2010.02.005.(in Chinese)

[6]ERLING M S.Nonlinear analysis of space trusses[J].Journal of Structural Engineering,1994,120(9):2717-2736.DOI:10.1061/(ASCE)0733-9445(1994)120:9(2717).

[7]KATO S,MUTOH I,SHOMURA M.Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J].Journal of Constructional Steel Research,1998,48(2/3):145-168.DOI:10.1016/S0143-974X(98)00199-0.

[8]SOHN S D,KIM S D,KANG M M.Nonlinear instability structures in civil engineering[C]//Proceedings of the IASS International Symposium.[S.l.: s.n.],2002:422-427.

[9]范峰,曹正罡,崔美艳.半刚性节点单层球面网壳的弹塑性稳定性分析[J].哈尔滨工业大学学报,2009,41(4):1-6.FAN Feng,CAO Zhenggang,CUI Meiyan.Elasto-plastic stability of semi-rigidity joint single-layer reticulated domes[J].Journal of Harbin Institute of Technology,2009,41(4):1-6.(in Chinese)

[10]马会环.半刚性节点单层球面网壳稳定性及其节点性能研究[D].哈尔滨:哈尔滨工业大学,2007.MA Huihuan.Study on stability and joint performance of single layer spherical reticulated shell with semi-rigid joints[D].Harbin: Harbin Institute of Technology,2007.(in Chinese)

[11]薛素铎,王宁,李雄彦.单层柱面网壳强震失效分析中考虑节点刚度影响的简化模型研究[J].振动与冲击,2013,32(16):106-111.DOI:10.13465/j.cnki.jvs.2013.16.033.XUE Suduo,WANG Ning,LI Xiongyan.Simplified model of single-layer cylindrical reticulated shell considering the effect of joint stiffness in failure analysis under strong earthquake[J].Journal of Vibration and Shock,2013,32(16):106-111.DOI:10.13465/j.cnki.jvs.2013.16.033.(in Chinese)

[12]范峰,马会环,沈世钊.半刚性型螺栓球节点单层K8型网壳弹塑性稳定分析[J].土木工程学报,2009,42(2):45-52.DOI: 10.15951/j.tmgcxb.2009.02.015.FAN Feng,MA Huihuan,SHEN Shizhao.Elasto-plastic stability analysis of K8 single-layer reticulated shells with bolt-ball joint system[J].China Civil Engineering Journal,2009,42(2):45-52.DOI: 10.15951/j.tmgcxb.2009.02.015.(in Chinese)

[13]范峰,马会环,沈世钊.半刚性螺栓球节点受力性能理论与试验研究[J].工程力学,2009,26(12):92-99.FAN Feng,MA Huihuan,SHEN Shizhao.Numerical simulation and experimental study on mechanical characters of bolt-ball joint system[J].Engineering Mechanics,2009,26(12):92-99.(in Chinese)

[14]曹正罡,范峰,马会环,等.螺栓球节点试验及在单层网壳结构中的应用性[J].哈尔滨工业大学学报,2010,42(4):525-530.CAO Zhenggang,FAN Feng,MA Huihuan,et al.Experiment of bolt-ball joint and its application in single-layer reticulated shells[J].Journal of Harbin Institute of Technology,2010,42(4):525-530.(in Chinese)

[15]中华人民共和国国家质量监督检验检疫总局.钢网架螺栓球节点用高强度螺栓:GB/T 16939—2016[S].北京:中国标准出版社,2016.General Administration of Quality Supervision,Inspection and Quarantine of the People's Republic of China.High Strength Bolts for Joints of Space Grid Structures: GB/T 16939—2016 [S].Beijing: China Standards Press,2016.(in Chinese)

[16]CHEN W F,KISHI N.Semi-rigid steel beam-to-column connections: data base and modeling[J].Journal of Structural Engineering,1989,115(1):105-119.DOI:10.1061/(ASCE)0733-9445(1989)115:1(105).

[17]LUI E M,CHEN W F.Analysis and behaviour of flexibly-jointed frames[J].Engineering Structures,1986,8(2):107-118.DOI:10.1016/0141-0296(86)90026-X.

[18]COLSON A.Connections incidence on the inelastic behavior of steel structures[C]//Euromech Colloquium.[S.l.: s.n.],1983:174.

[19]FRYE M J,MORRIS G A.Analysis of flexibly connected steel frames[J].Canadian Journal of Civil Engineering,1975,2(3):280-291.DOI:10.1139/l75-026.

[20]WU F H,CHEN W F.A design model for semi-rigid connections[J].Engineering Structures,1990,12(2):88-97.DOI:10.1016/0141-0296(90)90013-I.

[21]KISHI N,CHEN W F.Moment-rotation relations of semirigid connections with angles[J].Journal of Structural Engineering,1990,116(7):1813-1834.DOI:10.1061/(ASCE)0733-9445(1990)116:7(1813).

[22]范峰,曹正罡,马会环,等.网壳结构弹塑性稳定性[M].北京:科学出版社,2015:235-237.FAN Feng,CAO Zhenggang,MA Huihuan,et al.Elastoplastic stability of reticulated shell structures[M].Beijing:Science Press,2015:235-237.(in Chinese)