知识点：换流器

0 引 言

直流配电技术与传统交流配电技术相比，具有供电容量高、线性损耗小、电能质量高等优点[1?2]。此外，随着直流用电设备及分布式电源大量接入交流配电网，诸多的电力电子变换环节给交流配电网的安全可靠运行带来了影响。直流配电网能够更灵活地消纳直流负荷及分布式电源，必将会成为未来城市配电系统的重要组成部分。目前直流用电设备日益增多，为满足用电容量需求，采用换流器并联的直流配电拓扑结构，但直流配电系统固有的低惯性、弱阻尼特性易导致系统振荡，尤其采用并联换流器的拓扑时，需要进一步探究其振荡机理。

文献[3?5]研究了直流配电网振荡的原因，包括低阻尼 LC 环节与直流母线电压控制单元的交互作用、恒功率负荷的负阻抗效应、下垂系数的影响、多端互联的功率交互等；文献[6]首先建立多换流器并联系统的诺顿等效电路，定量分析谐振峰分布，求解谐振频率表达式，分析了系统参数对谐振的影响；文献[7]结合系统的阻抗模型和节点阻抗矩阵，提出基于阻抗的单母线谐振分析方法及系统级谐振分析方法分析谐振机理，并设计有源阻尼补偿器消除了谐振回路；文献[8]将两台逆变器与同类激励源合并为多逆变器并联系统小信号模型，分析谐振与逆变器控制和同步性之间的关系；文献[9]提出逆变器入网电流和滤波电容电流双闭环系统的输出阻抗建模方法，基于无 dq 环路阻抗耦合和引入数字控制延时逆变器输出阻抗模型，建立多逆变器并网系统的阻抗网络模型，分析谐振机理，发现逆变器产生谐波成分与电网电压谐波成分会加剧入网电流谐波畸变；文献[10]根据单台变流器诺顿等效电路定义其输出阻抗，基于阻抗法准确求解了多变流器并网系统的电网阻抗临界稳定值与失稳振荡频率。    

目前直流电压振荡现象的研究中，电压源型换流器

与恒功率负荷大多以级联的形式连接，所以普遍认为造成失稳的原因是恒功率负载的负阻抗特性，但在实际情况中，并联换流器间容易发生交互作用造成系统振荡，本文将着重从该点入手，得到 VSC_1作为激励源的系统 RLC并联回路，分析并联换流器系统的稳定性及振荡频率。

1 两换流器并联的直流配电系统稳定性模型

两换流器并联的直流配电系统的拓扑结构如图 1所示，两换流器均通过 P?Udc 下垂控制的方式实现功率均衡控制。为分析换流器并联方式的振荡机理，下文将建立换流器、直流线路和直流负荷的动态导纳模型，三部分共同构成完整的配电系统。

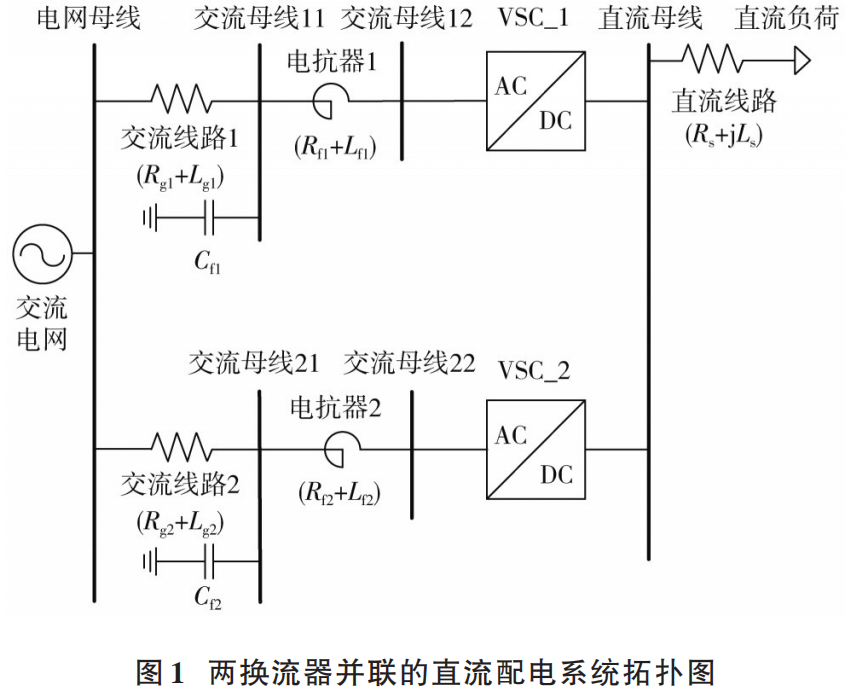
1.1 下垂控制原理    

直流配电系统是否稳定关键在于直流电压，因此本文选择 P?Udc 下垂控制，P?Udc指的是换流器输出有功功率和换流器直流侧电压之间的线性关系，利用该控制可以调节换流器的有功功率输出，并维持电压稳定 。P?Udc下垂控制原理如图2所示。

由下垂控制原理图得到换流器下垂表达式如下：

1.2 单个换流器的小扰动稳定性模型

单个换流器小扰动稳定性模型是指图 1 所示的电网母线与直流母线间整体部分的建模，即包括换流器、滤波器、交流线路、交流母线等部分。其中换流器采用下垂控制，控制框图如图3所示。

P?Udc 下垂控制运行在单位功率因数模式中，对直流侧有功功率作线性化小扰动，得到：

式中：Δ 表示某一时刻的运行值与稳定运行值的偏差；下标（0）表示稳定运行值；Ud为换流器输出交流电压在 d轴上的分量；Id是换流器输出交流电流在 d轴上的分量。考虑交流线路阻抗参数及滤波器对小扰动的影响，得到： 

式中：Rf,Lf 表示滤波器的电阻和电感，Cf 是与电抗器并联的接地电容，三者构成滤波器；Rg 和 Lg 是与电网母线直接相连的交流线路的电阻和电感；Uod 是与电网母线直接相连的交流母线的电压。

1.3 多换流器并联的小扰动稳定性模型

以两并联为例分析，其含义是两个换流器小扰动稳定性模型交流侧共同并接于电网母线，直流侧共同并接于直流母线，即换流器的并联是交流侧与直流侧都并联，换流器VSC_1和VSC_2均采用P?Udc下垂控制，因此，并联两换流器的小扰动稳定性模型表达式与式（4）相同，分别用ΔY1(s),ΔY2(s)表示，根据电路原理，并联电路总导纳等于各个支路的导纳之和，所以两并联换流器的小扰动稳定性模型为：

基于以上论述可知，根据单个换流器小扰动稳定性模型快速求解多换流器并联时小扰动稳定性模型，当 n 个换流器并联运行时，各个换流器小扰动稳定性模型为式（4），分别用ΔY1(s),ΔY2 (s)，…，ΔYn (s)表示，则多换流器并联的小扰动稳定性模型见式（6），该式表征了电网母线与直流母线间所有的换流器模型。

1.4 直流负荷及直流线路稳定模型

1）直流负荷稳定性模型

本文假定直流负荷功率恒定，直流负荷处的电流为：

式中 PL 是负荷有功功率。对式（7）做线性化小扰动，可以得到直流负荷的输出导纳为：

直流负荷的导纳为负值，表明其具有负阻抗特性，易导致系统不稳定，导纳幅值由负荷有功功率和直流母线电压两者决定。

2）直流线路稳定性模型

在本文中，采用π型集中参数等值电路模型代替直流线路，直流线路导纳 ΔYdcline (s)为：

因此，考虑负荷时的直流侧输出导纳，也即直流侧稳定性模型，表达式为：

对电压外环控制器在d轴上产生的电流信号参考值Idref及换流器产生的d轴调制解调信号 Pmd 作小扰动， 并联立式（2）和式（3），可得单个换流器交流侧的输入导纳，即小扰动稳定性模型表达式 ΔYdroop (s)如式（4）所示：

以图1中的直流母线为源荷分界点，多换流器并联的交直流互联配电系统的传递函数为直流侧负荷及线路的输出导纳与换流器交流侧输入导纳之比，式（11）为交直流配电系统稳定性分析的基础。

相关推荐链接：

1、异步电机软运行机理探究

2、同步发电机运行技术与实践