这篇文章,试图把桩基设计的逻辑介绍给一个外行,假设这个外行不太懂结构,我们该怎么办?我们用一个小报告,浅入深出地说明这个问题。 所有的行为,都对应特定的需求。桩基设计也不例外。 在桩基设计之前,应该先搞清楚,我们的需求是什么? 我们的需求是为上部结构找到一个(重力)支撑,将上部结构的重量传递至岩层或硬土层。桩是我们解决问题的工具。 而所谓的设计,其实是将需求实现,但代价最小化的一个过程。
这篇文章,试图把桩基设计的逻辑介绍给一个外行,假设这个外行不太懂结构,我们该怎么办?我们用一个小报告,浅入深出地说明这个问题。
所有的行为,都对应特定的需求。桩基设计也不例外。
在桩基设计之前,应该先搞清楚,我们的需求是什么?
我们的需求是为上部结构找到一个(重力)支撑,将上部结构的重量传递至岩层或硬土层。桩是我们解决问题的工具。
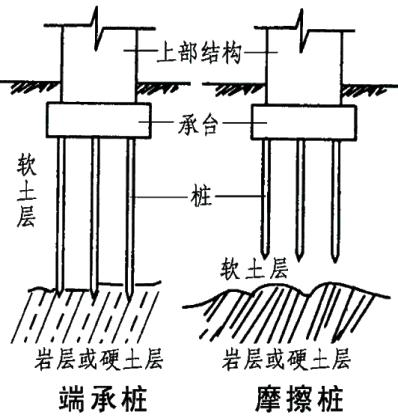
而所谓的设计,其实是将需求实现,但代价最小化的一个过程。
那代价是什么?
最显而易见的代价,就是我们在桩和承台上的花销。注意是桩和承台,而不仅仅是桩。
那如何使代价最小化?
从最朴素的力学常识来看,传力路径最短,代价最小。

单柱单桩,比单柱双桩(或单柱多桩),传力路径更短,所以代价更低。

将桩布置在剪力墙下,比大承台均匀布桩,传力路径更短,所以代价更低。
传力路径的优化,更多的是对承台的优化。接下来再看桩。
布桩,属于能力与需求的匹配问题。结构设计的需求是:能力≥需求,即桩承载力≥桩反力。桩的承载力利用率越高,结构代价越低。
从数学角度,桩的承载力(平均)利用率可以接近100%,但从工程角度,这是不可能的。
对一个实际工程来说,柱底总反力是确定的,但单个柱底反力的分布却是不均匀的,尤其是带裙房地下室的多塔结构。很多时候,这种反力分布的颗粒度是比较细的。
再看桩承载力。比如说,我们确定采用机械成孔灌注桩,桩径从1000~2200mm,每间隔200mm一个桩型,共7种,桩承载力特征值按桩身控制,承载力梯度一共就7种,承载力的颗粒度是比较粗的。
但我们用粗颗粒度的桩承载力去匹配细颗粒度的柱底反力,涉及到归并,承载力利用率一定是往下降的。
比如说1000mm的桩,其承载力特征值为7300kN,但某个柱底反力为7400kN,怎么办呢?我们只能匹配1200mm的桩,其承载力为10600kN,其承载力利用率为69.8%,以此类推,我们可以算出每个桩型的最低利用率。

整个项目,桩的平均承载力利用率最高的情况,无非是选择所有的桩型,但即使如此,利用率一定是低于100%的。同时,这会产生另一个问题。比如说,某些桩型,整个场地一共也就出现4、5根,或者小于10根,这会导致施工不便、检测费用更高、影响工期等问题,通常情况下,我们需要对桩径继续归并,尽量采用较少的桩径种类。
但桩径归并, 会进一步降低桩的承载力利用率。比如,我们最终选择了1000mm、1200mm、1600mm、2000mm共四种桩型,如果某根柱的柱底反力是11000kN,大于1200mm桩的承载力,只能选择1600mm的桩型,其承载力为18800kN,对应的利用率仅为58.5%.
桩径归并,其实是在桩利用率和便利性之间做一个平衡。
这么看来,桩基设计其实是一个数学问题。当我们确定了柱底反力,桩、承台的各项成本,检测成本、受力要求等边界条件,我们可以通过线性优化工具,找到最优的桩型、最合理的桩径种类以及桩布置。
但从真实的工程角度来看,这是一个多边界条件、多目标的,模糊线性优化问题。
如果说结构传力的代价,这个边界条件是一个白箱子,那各种成本因地域和具体的施工承包商而异,其实算是一个灰箱子;

而结构受力安全度的控制,比如规范规定的参数是0.7~0.9,用0.7,0.8,还是0.9,因设计单位和设计师而异;桩间距控制,配筋率控制也和设计师及审图要求相关;对建筑条件不确定性的评估、施工工艺的地域性限值、工期的敏感性等,基本是主观性的判断,这些边界条件更加模糊,算是更灰色的箱子。

但这个灰箱子可能影响更大。比如,建筑考虑后期加建的可能,要求桩基设计预留更大的富裕度;比如,建设方规定的最大桩型为2.2m,对一栋250m的塔楼,可能无法实现外框柱的单柱单桩布置等。或者因为施工时间紧迫,桩基设计时间过短,根本没有优化时间等。
所以,桩基设计的边界条件是多个的,且有些是偏主观、偏模糊的。
再来看桩基设计的目标。
最可以量化的目标,其实是桩、承台的结构成本,其次是土方、施工的成本。
但还有一些隐含的目标,比如风险可控,工期可控;同样的一个项目,如果场地孤石较多,虽然预应力管桩的成本较低,但基于施工风险和工期控制,更多情况下,可能会采用成本较高的灌注桩。
再比如,耐久性好。单纯从成本角度考虑,抗浮措施可以采用布置排水盲沟的方式,但基于耐久性考虑,可能会采用抗拔桩。

所以,桩基设计的目标,其实也是多个的,有些也是模糊,甚至偏主观的。
对一个多边界条件、多目标的,模糊线性优化问题。我们没有办法采用纯数学的方式将其求解。即使在工程角度,对这类问题,没有绝对最优解,只有相对较优解。
如果不同的设计目标用fi(x)表示,桩基设计可以用下面的数学模型表示,我们的整体目标是F(x),多目标优化的困难就在于,我们无法实现每个fi(x)最优,因为f1(x)最优,可能要以牺牲f2(x)为代价,甚至以f3(x)和f4(x)为代价。

对这类问题,较优解会有多个。在不同的关注点上,这些解各有利弊。
合理的设计,其实就是首先去掉不可行解,在可行解里面,通过方案对比、经验判断、结构计算、成本估算等方式,基本保证我们给出的方案落在满意解的区间。这是一个客观+主观的决策过程。

桩基设计的逻辑,其实也是结构设计的逻辑。在不确定性中寻找确定性,在确定性中评估不确定性。
桩基设计的逻辑,也许三言两语可以讲完。但如何让外行理解这个问题,同时也认可我们的专业度,这是一门学问。
内容源于网络,仅作分享使用,如有侵权,请联系删除
相关资料推荐:
18层剪力墙结构住宅楼结构设计施工图(桩基础)
某三层展览馆核心筒结构大门结构设计施工图(桩基础)
知识点:桩基设计逻辑
