“索杆体系”是指由“索”单元或“杆”单元组成的结构体系,初始状态内力仅需满足平衡条件;“索梁体系”是指由“梁”和“索”(或“杆”)组成的体系,初始状态梁部分的内力是由自零状态至初始状态的变形引起的,所以不仅需满足平衡条件还需满足变形协调条件。 几何不协调的变形意味着在主动索张拉过程中有部分索段张紧受力而其他索段处于松弛状态。对于几何不协调变形的情况,如果设计几何给定,满足平衡条件的任意一组预张力分布均可作为初始状态的预张力;如果设计几何不定,满足给定支承几何和边界条件的设计几何及其对应的一组平衡预张力可以作为结构的初始状态。几何协调的变形意味着在主动索张拉过程中各构件同时受力,产生几何协调变形最终达到初始状态,在初始状态索结构的预张力分布既满足平衡条件同时又满足几何协调条件。
“索杆体系”是指由“索”单元或“杆”单元组成的结构体系,初始状态内力仅需满足平衡条件;“索梁体系”是指由“梁”和“索”(或“杆”)组成的体系,初始状态梁部分的内力是由自零状态至初始状态的变形引起的,所以不仅需满足平衡条件还需满足变形协调条件。
几何不协调的变形意味着在主动索张拉过程中有部分索段张紧受力而其他索段处于松弛状态。对于几何不协调变形的情况,如果设计几何给定,满足平衡条件的任意一组预张力分布均可作为初始状态的预张力;如果设计几何不定,满足给定支承几何和边界条件的设计几何及其对应的一组平衡预张力可以作为结构的初始状态。几何协调的变形意味着在主动索张拉过程中各构件同时受力,产生几何协调变形最终达到初始状态,在初始状态索结构的预张力分布既满足平衡条件同时又满足几何协调条件。
(一)索杆体系
3D3S软件对于几何给定“索杆体系”的初始状态确定提供了两种方法∶矩阵分析法和有限单元法。矩阵分析法可得到严格满足给定几何的“索杆体系”的预张力分布,计算简单方便,其应用的前提是在给定几何上“索杆体系”满足平衡条件。当无法满足时,可采用有限单元法进行计算以寻找修正的几何及对应的平衡内力。3D3S软件的有限单元方法中,可定义主动索、被动索以及相应的预张力值。迭代计算中,主动索的预张力值保持不变,刚度值不参与结构总刚度组装;被动索的内力可根据其两端位移进行修正,单元刚度参与总刚度组装。显然,这样的计算完全符合结构施工张拉的实际情况。
矩阵分析法
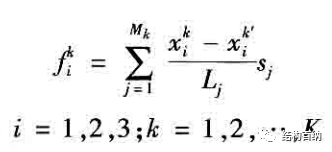
|

|

|
|
索杆体系形状确定是定义若干构件预张力,软件根据力的平衡条件找到一组符合条件的预张力分布。不能将所有杆件都定义预张力,除非所定义的预张力本身是平衡的,否则将软件提示“定义了多余杆件预张力,不能得到预张力分布”。
根据力的平衡条件,可以将所有杆件的内力求出。在此条件下,结构体系有唯一的预张力分布。
当力的平衡条件并不能得到唯一的预张力分布。在此条件下,软件假定一组预张力分布,通过最小二乘法得到符合条件的预张力分布。假定构件中所设的最大预张力为 P,则软件假定的预张力分布为:所有未设预张力的拉杆内力为 P,所有压杆为-P。
索杆体系设定的预张力必须为主动索,若设为被动索,软件认为没有定义杆件预张力。
索杆体系计算不得有梁单元的参与,否则软件退出计算。
索杆体系形状确定的建模位置为初始态位置,表示在建模位置上有一组符合初始设定预张力条件的平衡预张力分布。
(二)索梁体系
“索梁体系”是指随主动索预张力的施加而协调变形的结构体系,张弦梁、斜拉和悬挂梁屋盖及弦支穹顶等都是典型的“索梁体系”。“索梁体系”中刚性屋盖的标高、跨度等一般是设计事先确定的,结构张拉完成后的初始状态几何应符合图纸几何的要求。
采用数值方法进行“索梁体系”找形分析时,必须首先建立结构分析模型,存在以下两种情况∶
2.1初始状态几何等于图纸几何
一般要求索结构施工张拉完毕后的初始状态几何严格满足图纸几何的要求。这时,“索梁体系”的找形分析就是寻找与图纸几何对应的结构体系的一组平衡预张力分布。而结构的零状态几何不能直接按图纸几何取用,必须在图纸几何基础上释放预张力进行计算得到。
当预张力产生的位移效应与自重产生的位移效应可以相互抵消时或当预张力张拉引起的结构变形很小时,可取零状态几何为图纸几何,在此基础上计算结构的初始状态几何及其对应的平衡预张力分布。
当结构施加预张力的效应与自重效应相互抵消、或结构张拉引起的变形很小时,可将图纸几何取为零状态几何,在此基础上施加预张力和自重,直接进行非线性计算得到结构的初始状态几何和内力,如图7-3所示。这样实现的初始状态几何与图纸几何的偏差不会很大。因为计算是在给定的图纸几何基础上进行的,直接采用几何非线性有限单元方法可以精确计算得到结构的初始状态,这一方法称为非线性直接分析法,适用于零状态几何等于图纸几何的情况。

通用有限单元软件在计算“索梁体系”的初始状态时,可根据图纸几何建模,在此基础上施加预张力进行非线性计算得到结构变形后的初始状态几何和内力分布。显然,通用有限单元软件实现的是上述第2种情况。但是,通用有限单元软件没有保持主动索力不变的功能,必须经多次试算成功后才能使主动索段的内力符合给定的主动索力值。
3D3S软件对“索梁体系”初始状态的确定提供了实现上述第1和第2种情况的功能,计算中过程中可保持主动索力不变。
撤杆加力法-初始状态几何等于图纸几何-近似位移协调原则

|

|
在图7-1中,主动索预张力为Sl,结构体系的预张力分布应该是与主动索力Sl,及结构自重自相平衡的。当按图纸几何建立结构模型后,为了求解与图纸几何对应的平衡内力分布,可以撤除主动索,在其两端施加力Sl,按线性方法计算与Sl,和自重对应的结构内力分布,这组结构内力分布就是结构初始状态的预张力分布,而与之对应的初始状态几何就是图纸几何 。“索梁体系”初始状态找形分析的这一方法称为撤杆加力法,适用于初始状态几何取图纸几何的结构体系。
首先建立所有单元(包括索单元)的线性有限单元方程,但在组装总刚时忽略给定预张力 {Sl} 的1根索段的刚度贡献,并将{Sl}和自重作为外力施加到对应的索段两端节点处(如图7-1中右图所示)。求解相应的有限单元方程,得到相对应的与{Sl}及自重平衡的其他单元内力分布,所求内力为预张力分布。
按撤杆加力法计算得到的预张力分布在给定的几何位置上能严格满足平衡条件。
精确位移协调原则

|
实线的初始状态是确定的,需要通过有限单元法反求结构的零状态及结构的预张力分布,计算步骤如下:
I. 结构初始状态几何位置{X,Y,Z}是给定的。假定结构的初始状态就是结构零状态,几何位置坐标{X0,Y0,Z0}= {X,Y,Z}:
II.在假定的零状态基础上,建立非线性有限单元方程,与近似位移协调相似,不考虑施加预张力的单元刚度贡献,同时将预张力考虑为一对相向力;
III.通过几何非线性迭代计算,消除结构不平衡力,得到结构最终位置是假定零状态结构在预张力作用下的初始态位置,位移向量{U0},也就是新的初始状态位置为{Xo,Yo,Zo}+{Uo};
IV.如果{Xo,Yo,Zo}+{Uo}一{X,Y,Z}在给定精度范围内说明结构零状态找到,结构的内力分布即为预张力的分布,否则取{Xo,Yo,Zo } ={X, Y,Z}一{Uo}为新的结构零状态,返回到II重新计算。
根据精确位移协调原则求到的初始状态结构预应力分布是严格满足平衡条件的,并且严格符合结构自零状态至初始状态的位移协调条件,而且应用这一原则在求出给定初始状态几何的结构预应力分布的同时也求出了结构零状态的放样几何。
2. 零状态几何等于图纸几何

|
零状态几何给定的结构需要通过精确位移协调原则确定结构的初始状态。
图所示的实线结构是结构的零状态,施加预张力后得到 “起拱”后的初始状态 用虚线表示。由于结构零状态已知,初始状态末知,可以将初始状态确定看成墓本的非线性分析的过程,具体步骤为:
I. 结构零状态几何位置(Xo,Yo,Zo}给定:
II.在给定的零状态的基础上,建立非线性有限单元方程,不考虑施加预张力的单元刚度贡献,同时将预张力考虑为一对相向力;
III.通过几何非线性迭代计算,消除结构的不平衡力。这一计算过程中产生的不平衡力,不仅是由于结构位形变化引起的,同时也包括预张力索 (拉杆)位形变化造成的预张力方向变化而产生的不平衡力;
IV.得到结构的最终变形后的位置就是结构的初始状态位置
零状态给定的精确位移协调原则只能适用于刚度较大的半刚性结构,如斜拉结构等。因为对于这类结构,由于施加预应力引起的自零状态至初始状态的几何变化不大,初始状态几何与设计图纸中给定几何相差不会太大,从而不会对结构外观有太大影响,也不会导致安装施工的困难。
同初始状态几何给定的精确位移协调原则相比,采用本节零状态几何给定的原则进行形状确定更为简单,只需进行一次非线性迭代计算就可将预应力作用下的初始状态几何及相应的平衡内力(预应力)求解出来。
软件:索梁体系初始状态的位移显示体现了结构零状态和初始状态之间的位置关系。当结构的建模位置是初始状态时,显示位移后的结构位置为结构零状态的位置;当结构的建模位置为零状态时,显示位移后的结构位置为结构初始状态的位置。
知识点:索杆体系和索梁体系
