地震动是场地的往复运动，在地震中结构以及结构组成构件也经历了往复变形。了解结构和构件的滞回性能及其影响因素能够优化构件配筋构造，改善结构性能，而选取合适的滞回分析模型，对分析预测结构极限状态性能有着重要意义。

滞回是一种普遍存在的非线性现象，对于结构工程领域材料、构件或结构在往复荷载作用下的广义力-变形关系就是滞回模型（hysteretic model）或称为恢复力模型。恢复力也指构件或结构在外荷载去除后恢复原来形状的能力。

构件滞回曲线的实验数据一般由低周期反复试验获得，这些试验开始于上个世纪50年代后期。该试验方式至今仍应用在新材料、新型构件或结构的非线性滞回研究。

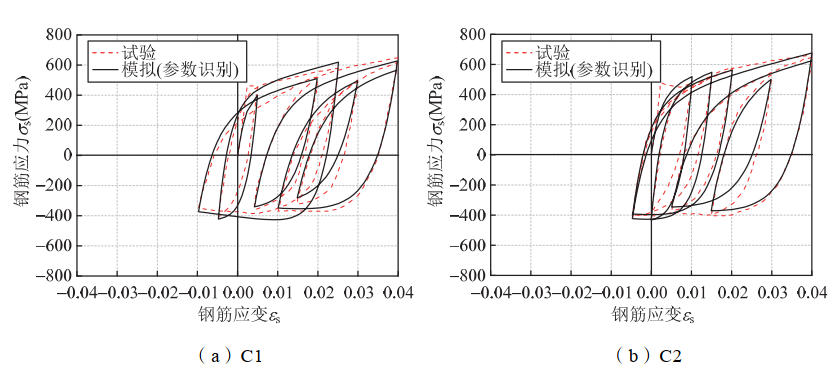
图 1：钢筋滞回本构（试验vs 参数识别）

图片来源：仇建磊, 贡金鑫. 考虑屈曲影响的钢筋滞回本构模型 [J]. 土木工程学报, 2019, 52(2): 11.

图 2：叠合剪力墙滞回试验与OpenSees 分析结果对比

图片来源：余少乐, 杨联萍, 张其林, et al. 双面叠合剪力墙恢复力模型与有限元分析 [J]. 建筑结构, 2019, 049(002): 20-8.

上图1为考虑屈曲影响的钢筋滞回曲线，上图2为新型双面叠合剪力墙 试验得到的滞回曲线与数值模型分析对比。

滞回曲线的外包络线称为骨架曲线，骨架曲线能够反映在往复加载过程中的强度刚度变化特征，进而定义各个性能点；在多数情况下，滞回模型与推覆试验（Pushover）获得的力-位移曲线基本一致。对于一般结构构件，往复加载过程中会表现为强度、刚度退化，退化性质反应构件累积损伤的影响；一般来说混凝土构件的退化较钢构件严重。

当结构或构件进入非线性，加载路径与卸载路径不重合时就会形成滞回环，滞回环所包络面积能够反映构件或结构的能量耗散特性，而对各阶段滞回环形态以及形态变化的分析可以帮助评估结构或构件的性能状态。单个滞回环的典型形状一般有三种:梭形、弓形、倒S形[5]：

图 3：滞回环典型形状

图片来源：何政, 欧进萍. 钢筋混凝土结构非线性分析 [M]. 钢筋混凝土结构非线性分析, 2007

其中梭形形状饱满，代表无剪切破坏机制。如受弯构件、无滑移的偏压、压弯等，耗能能力最好；弓形中部存在"捏缩"效应，代表受一定剪力以及钢筋粘结滑移影响的构件，滞回曲线的形状比较饱满，但饱满程度比梭形要低，反映出整个结构或构件的塑性变形能力比较强；倒 S形反映出滞回曲线受到了大量的滑移影响，耗能能力最弱。例如小剪跨而斜裂缝又可以充分发展的构件以及锚固钢筋有较大滑移的构件等，其滞回曲线都属此类。

构件的滞回特征

1、钢筋混凝土梁的滞回特性

梁的滞回特性取决于其破坏方式。如果梁的破坏形式为受弯破坏，则钢筋屈服前的滞回曲线基本呈梭形，钢筋屈服后，由于钢筋的包兴格效应、裂缝的张开闭合，滞回环将出现捏拢特征，刚度退化也会变得明显。如果梁的破坏形式为受剪破坏，滞回曲线将出现显著的捏拢特征。

图 4：受弯构件典型滞回曲线

图片来源：李杰, 李国强. 地震工程学导论 [M]. 地震工程学导论, 1992.

2、钢筋混凝土柱

钢筋混凝土柱的滞回曲线特征受轴压比、配箍特征值、剪跨比、混凝土强度等级、纵筋配筋率以及构件截面形状等因素影响，其中轴压比、配箍特征值和剪跨比的影响最为显著 []。随着轴压比的增大，构件的极限承载力（骨架曲线峰值点）先增加后下降，滞回曲线出现越来越强的捏拢特征，变形和耗能能力迅速降低。此外，随着轴压比的增大，柱在纵筋屈服后的承载力和刚度衰减特性也越来越明显。提高纵筋配筋率，能够显著提高极限承载力、降低捏拢效应，改善耗能能力和延性。提高构件配箍率，虽然不能提高构件的极限承载力，但是滞回曲线变得更加丰满，耗能能力增强，极限变形增大，延性性能改善明显。因此，在抗震设计中严格配箍率要求有着重要的工程意义。柱的长细比对柱的承载力和滞回性能有着较大影响。当柱的长细比增大时，其承载力下降，但滞回曲线较为丰满，此时的柱滞回性能受配筋率和配箍率影响较大。

图 5：荷载-柱顶位移滞回曲线

图片来源：李军涛, 陈宗平, 王欢欢, et al. 钢筋混凝土柱压弯剪扭滞回性能试验研究 [J]. 土木工程学报, 2018, 051(007): 87-97.

框架节点滞回性能

节点受力最为复杂，节点的承载力和滞回特性取决于梁、柱内力的比例、轴压比、节点内纵筋数量和箍筋构造、钢筋的锚固措施等。

图 6：节点受力状态及滞回曲线

图片来源：何政, 欧进萍. 钢筋混凝土结构非线性分析 [M]. 钢筋混凝土结构非线性分析, 2007.

混凝土框架节点随着配箍特征值增加，延性增大，但当配箍特征值超过规范值后，其延性系数和耗能能力增加不明显。混凝土框架节点在剪压比低于0.3 时，延性系数和耗能能力变化不大；当剪压比高于 0.3 后，延性系数和耗能能力下降较快。当剪压比过大时，按规范配置箍筋也不能防止节点发生剪切破坏。混凝土框架节点轴压比低于0.5 时，延性系数随轴压比增大而提高；轴压比高于 0.5 时，延性随着轴压比增大而下降，且耗能能力下降较快。因此，当轴压比过大时，轴压比对节点抗剪强度的有利作用减小，延性降低[]。

钢筋混凝土剪力墙滞回性能

剪力墙的受力状况类似于悬臂梁，其上的洞口对其整体受力性能的影响不大 ，但对局部构件的性能影响较大，如墙股、连系梁等。影响剪力墙滞回特性的关键因素是剪跨比。当剪跨比较大时，其呈现弯曲破坏形态，滞回曲线呈梭型，耗能能力较强；当剪跨比较小时，其呈现剪切破坏形态，滞回曲线呈捏拢特征，耗能能力较弱，如下图7所示。

图 7：剪力墙的滞回特征

图片来源：何政, 欧进萍. 钢筋混凝土结构非线性分析 [M]. 钢筋混凝土结构非线性分析, 2007.

数值滞回模型

数值滞回模型，是将滞回行为用一组数学公式描述。公式形式在对物理现象的观测和分析基础上抽象和简化得出，而公式参数则由大量回归分析或根据参数物理意义计算得出。数值滞回模型首先应该能体现结构或构件的滞回性能，其次在数值仿真中应易于处理。滞回模型按照数学表达式定义方式的不同可分为折线形模型和光滑型模型。完整的折线型恢复力模型，由骨架曲线和滞回规则两部分定义组成，根据骨架曲线上折线的数目，折线型恢复力模型又可细分为双线性、三线性和四线性等模型。折线型恢复力模型由于在动力分析中刚度修正次数少，但存在着拐点处理的问题。

在过去的六十多年中，在大量试验的基础上提出了多种恢复力模型。双线性(Bi-linear)模型最早由Penizen等在1962年提出，模型针对钢材提出，具有简单实用的优点，因而应用广泛。Clough和Johnston在双线性模型基础上，考虑再加载时刚度退化提出了退化双线性模型Clough模型，如图8所示。1970年，Takeda（武田）、Sozen和Nielson[]根据大量钢筋混凝土构件的滞回特性,利用一条考虑开裂、屈服的三折线骨架曲线和一系列较为复杂的滞回环规则对Clough模型进行了改进，该模型最大的特点是考虑了卸载刚度的退化。Takeda（武田）模型如图9所示。

图 8：Clough 模型   

图 9 ：Takkeda 模型

Saiidi[4]结合Clough模型的定义简单和Takeda模型的刚度退化特征，建立了一个既简便实用又能基本反应以弯曲变形为主的滞回特征模型(Q-hyst Model)。

图 10：Q-hyst Model 模型

图片来源：SAIIDI M. Hysteresis Models for Reinforced Concrete [J]. Journal of the Structural Division, 1982, 108(5): 1077-87.

光滑型模型同折线型模型相比在计算过程中需不断对单元刚度矩阵进行修正，但避免了拐点处理。其中Bonc-Wen模型和Ramberg-Osgood模型应用较为广泛。其他光滑型滞回模型包括Duhem 模型、用于弹塑性材料分析的Ishlinskii滞回模型等。

图 11 Bouc-Wen模型的滞回响应

参考文献：

[1] 杨红, 白绍良. 基于变轴力和定轴力试验对比的钢筋混凝土柱恢复力滞回特性研究 [J]. 工程力学, 2003, 20(6)

[2] 唐昌辉, 朱孝辉. 混凝土框架节点滞回性能研究 [J]. 铁道科学与工程学报, 2018, 015(006): 1534-41.

[3] TAKEDA T. Reinforced Concrete response to simulated earthquakes [J]. Journal of the Structural Division Proceedings of the American Society of Civil Engineers, 1970, 96(2557-73.

[4] SAIIDI M. Hysteresis Models for Reinforced Concrete [J]. Journal of the Structural Division, 1982, 108(5): 1077-87.

[5] 何政, 欧进萍. 钢筋混凝土结构非线性分析 [M]. 钢筋混凝土结构非线性分析, 2007.

[6] 李杰, 李国强. 地震工程学导论 [M]. 地震工程学导论, 1992.