受弯构件承载力计算是一个极为极为复杂的问题。小编也是查了很多资料，看了上百篇论文后才知道的。国内外目前为止各类构件的受剪承载力试验累计已经做了几千个，亲们，几千个，也没有提出一个能普遍认可能广泛适用的破坏机理、破坏模式和计算理论。目前，斜截面受剪的破坏机理和计算理论主要有：拉杆拱模型、平面比拟桁架模型、变角桁架模型、拱-梳状齿模型、极限平衡理论等等。各位有兴趣就在网上搜索搜索。有些计算模型太复杂，无法在工程设计中得到应用。

受弯构件承载力计算是一个极为极为复杂的问题。小编也是查了很多资料，看了上百篇论文后才知道的。国内外目前为止各类构件的受剪承载力试验累计已经做了几千个，亲们，几千个，也没有提出一个能普遍认可能广泛适用的破坏机理、破坏模式和计算理论。

目前，斜截面受剪的破坏机理和计算理论主要有：拉杆拱模型、平面比拟桁架模型、变角桁架模型、拱-梳状齿模型、极限平衡理论等等。各位有兴趣就在网上搜索搜索。有些计算模型太复杂，无法在工程设计中得到应用。

我国设计规范中，斜截面受剪承载力计算主要依据极限平衡理论，当然也是经过大量的实验，理论结合实际建立起来的。其特点是考虑的因素较少，计算简便。但是与一些国家的规范相比，其安全度水平是不高的。

基本假定和基本计算公式

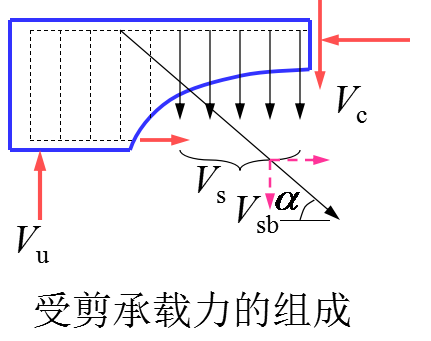
1）假定梁的斜截面受剪承载力Vu由斜裂缝上剪压区混凝土的抗剪能力Vc，与斜裂缝相交的箍筋的抗剪能力Vsv和与斜裂缝相交的弯起钢筋的抗剪能力Vsb三部分所组成（如下图）。

由平衡条件∑Y=0可得：

Vu= Vc +Vsv+Vsb

如令Vcs为箍筋和混凝土共同承受的剪力，即

Vcs=Vc+Vsv

则 Vu=Vcs+Vsb

2）梁剪压破坏时，与斜裂缝相交的箍筋和弯起钢筋的拉应力都达到其屈服强度，但要考虑拉应力可能不均匀，特别是靠近剪压区的箍筋有可能达不到屈服强度。

3）斜裂缝处的骨料咬合力和纵筋的销栓力，在无腹筋梁中的作用还较显著，两者承受的剪力可达总剪力的50%~90%，但试验表明在有腹筋梁中，它们所承受的剪力仅占总剪力的20%左右。

4）截面尺寸的影响主要对无腹筋的受弯构件，故仅在不配箍筋和弯起钢筋的厚板计算时才予以考虑。

5）剪跨比是影响斜截面承载力的重要因素之一，但为了计算公式应用简便，仅在计算受集中荷载为主的梁时才考虑了λ的影响。

斜截面受剪承载力的计算公式

1．均布荷载作用下矩形、T形和I形截面的简支梁，当仅配箍筋时，斜截面受剪承载力的计算公式

2．对集中荷载作用下的矩形、T形和I形截面独立简支梁当仅配箍筋时，斜截面受剪承载力的计算公式

3．配有箍筋和弯起钢筋时梁的斜截面受剪承载力，其斜截面承载力设计表达式为：

4．不配置箍筋和弯起钢筋的一般板类受弯构件，其斜截面的受剪承载力应按下列公式计算

βh------截面高度影响系数，当h0小于800mm时，取h0等于800mm；当h0大于2000mm时，取h0等于2000mm。

计算公式的适用范围

上限值—最小截面尺寸

当hw/b≤4.0时，属于一般的梁，应满足

当hw/b≥6.0时，属于薄腹梁，应满足

当4.0＜hw/b<6.0时，属于薄腹梁，应满足

下限值—箍筋最小含量

为了避免发生斜拉破坏，《规范》规定，箍筋最小配筋率为

计算步骤

斜截面受剪承载力的计算按下列步骤进行设计：

1.求内力，绘制剪力图；

2.确定斜截面承载力计算的截面位置。斜截面受剪承载力计算时，需对下列截面进行计算。

（1）支座边缘的斜截面（见下图的截面1-1）

（2）箍筋直径或间距改变处的斜截面（见下图的截面4-4）

（3）弯起钢筋弯起点处的斜截面（见下图截面2-2、3-3）

（4）腹板宽度或截面高度改变处的斜截面（如下图的截面5-5）

以上这些斜截面都是受剪承载力较薄弱之处，计算时应取这些斜截面范围内的最大剪力，即取斜截面起始端处的剪力作为计算的外剪力。

3.验算是否满足截面限制条件，如不满足，则应加大截面尺寸或提高混凝土的强度等级；

4.验算是否需要按计算配置腹筋。

5.计算腹筋

（1）对仅配置箍筋的梁，可按下式计算：

对矩形、T形和工字形截面的一般受弯构件

对集中荷载作用下的独立梁

（2）同时配置箍筋和弯起钢筋的梁，可以根据经验和构造要求配置箍筋确定Vcs，然后按下式计算弯起钢筋的面积。

也可以根据受弯承载力的要求，先选定弯起钢筋再按下式计算所需箍筋：

然后验算弯起点的位置是否满足斜截面承载力的要求。

保证斜截面受弯承载力的构造措施

抵抗弯矩图的概念

抵抗弯矩图就是以各截面实际纵向受拉钢筋所能承受的弯矩为纵坐标，以相应的截面位置为横坐标，所作出的弯矩图（或称材料图），简称Mu图。

当梁的截面尺寸，材料强度及钢筋截面面积确定后，其抵抗弯矩值，可由下式确定

保证斜截面受弯承载力的构造要求

1．纵向钢筋的弯起

对梁纵向钢筋的弯起必须满足三个要求：

①满足斜截面受剪承载力的要求。

②满足正截面受弯承载力的要求。设计时，必须使梁的抵抗弯矩图不小于相应的荷载计算弯矩图；

③满足斜截面受弯承载力的要求，亦即上面讨论的当纵向钢筋弯起时，其弯起点与充分利用点之间的距离不得小于0.5h0；同时，弯起钢筋与梁纵轴线的交点应位于按计算不需要该钢筋的截面以外。

2．纵向钢筋的截断

在设计时，为了避免发生斜截面受弯破坏，使每一根纵向受力钢筋在结构中发挥其承载力的作用，应从其“强度充分利用截面”外伸一定的长度ldl，依靠这段长度与混凝土的粘结锚固作用维持钢筋以足够的抗力。同时，当一根钢筋由于弯矩图变化，将不考虑其抗力而切断时，从按正截面承载力计算“不需要该钢筋的截面”也须外伸一定的长度ld2，作为受力钢筋应有的构造措施。在结构设计中，应从上述两个条件中确定的较长外伸长度作为纵向受力钢筋的实际延伸长度ld，作为其真正的切断点。

钢筋混凝土连续梁、框架梁支座截面的负弯矩纵向钢筋不宜在受拉区截断。如必须截断时，其延伸长度ld可按下表中ld1和ld2中取外伸长度较长者确定。其中ld1是从“充分利用该钢筋强度的截面”延伸出的长度；而ld2是从“按正截面承载力计算不需要该钢筋的截面”延伸出的长度。