i-d 向量空间与舒适性空调系统运行性能的计算

把焓湿图视为i-d向量空间以及把空调机组视为向量函数，空调系统就成为一个数学体，空气处理过程可以以向量函数公式来表示。于是空调系统在任意室外工况和室内负荷下的运行性能参数都可以做数学计算，空调学就从实验科学转变成理论科学。这么一来空调系统设计也呈现崭新的思维方式和方法（paradigm）。接着本文利用i-d向量空间理论计算一个集中新风舒适性空调系统在设计、恶劣和梅雨工况的运行性能参数，焦点为室内相对湿度。

关键词

焓湿图, i-d向量空间, 选型软件, 性能计算, 室内热负荷, 湿负荷，负荷向量, 室内平衡状态点. 舒适性空调，恶劣工况，梅雨工况。

摘要

在设计室外工况点和室内负荷下，常规焓湿图或i-d图可做设计和冷量或风量计算。这是一个世纪前美国人开利（Willis Carrier）所以被誉为空调之父所做的贡献。然而焓湿图存在一个极大的局限，那就是应用焓湿图设计好的一个空调系统，一旦改变了室外工况或室内负荷，其运行性能就无法做理论计算。于是就只能寄托于实验、现场搜集大数据和经验，所以空调学仍然停留在经验科学的阶段。

本文提出i-d向量空间的理论并应用于计算一个常规集中新风舒适性空调系统在各种工况下的运行性能参数。在随后的文章里我们将应用i-d向量空间理论计算，准确设计比常规7-12℃供回水的空调系统性能更优越和节能接近10%的7-15℃供回水大温差小水流量空调系统。

经验科学的一个特点是存在比较多不容易通过繁琐的实验来证明的猜想。本文尝试通过i-d向量空间理论计算来讨论和否定其中一个因为无知而造成中央空调系统无谓耗能的猜想，那就是提高水温将提高室内相对湿度的猜想。

i-d向量空间的观点借鉴牛顿对物理学的贡献，那就是把物理系统数学化。以最简单的等加速度线性运动物理系统为例，当一个固定的外力F作用在一个质量m的物体上，此物理系统为 F=ma。

如果加速度a 并非数学体，则无法做数学运算。因此在牛顿发明微积分之前，物理学一直停留在经验科学 的阶段。直到牛顿发明微积分，以x”(t)表示a，于是物理系统可以表示为F=mx”(t) 。两次积分就可得位移x=ut+1/2at2。

迄今，空调系统并非一个数学系统。有人认为1979年Dhar M, Soedel W  [3] 所提出的微元模型是答案。其实微元模型固然适用于制冷系统与其配件的建模，但是并不适合于空调系统。明显的原因是空调系统所牵涉的是热湿处理的宏观层面，而并非制冷系统所牵涉的微观热交换过程。或者说空调系统所牵涉的层面是焓湿图的层面，并非压焓图的层面。

对应空调系统而言，建立微元模型属于数值模型（numerical model）而并非分析模型（analytical model），其缺陷是其中物理性质多隐藏于繁琐的数值计算中。

本文的首要任务是把焓湿图转变成为数学体。以焓值坐标取代干球温度坐标，焓湿图就自然而然地成为一个向量空间。再把热湿负荷的焓值和含湿量表示成负荷向量，仅存的工作就是把空调机组以数学表示。在盘管选型软件内输入空调机组的结构参数，这个在i-d向量空间上的函数就是空调机组的数学表示（mathematical representation)。

完成了整个空调系统的数学化，于是就能计算空调系统在任意室外工况和室内负荷下运行的性能。其结果是空调学就从经验科学转变成为理论科学。

1i-d 向量空间

定义:  i-d 向量空间 (Ω, +, *) 是以焓值i和含湿量d作为坐标轴的焓湿图。空气状态点为Ω中的向量，例如 室内空气状态点N = (iN, dN)。运算 +, * 是向量之和以及标量乘积。负荷向量是自由向量 Δ = (Δi, Δd) ，Δi 为热负荷的焓值，Δd 为湿负荷的含湿量。空调系统是以输入结构参数的选型软件所表示的一个向量函数 F :Ω↗Ω 。 (例如图2的左图)。

i-d向量空间与i-d图（焓湿图）的第一个差异是以焓值坐标替代干球温度坐标，于是空气状态点可以表示为一个二维向量X= (iX kJ/kg, dX g/kg)。室内热负荷与湿负荷也可以表示为负荷向量 Δ = (Δi, Δd)。于是空气状态点之间以及与负荷向量的向量加减和标量乘除运算完全成立，空调设计不再需要画热湿比线。

然而要把整个空调系统转变成为数学系统，上述举措并不充分。关键是还必须把空调机组转变成为数学体。以输入结构参数的表冷器选型软件来表示空调机组即可完成任务。严格说表冷器选型软件应称为空调机组选项软件。

把空调系统以数学表示后，空调系统在任意室外工况和室内负荷下的运行性能参数于是就可以做数学计算。或者说空调学于是就从经验科学转变成理论科学。下面我们以一个常规集中新风舒适性空调系统的案例来详细阐述i-d向量空间理论。

项目: 南京一会议室, 空间:16m x 10m x 3m; 南墙16m x 3m; 南窗16m x 1.5m; 天花板16m x 10m;  地面 16m x 10m; 内墙 36m x 3m;  内门 6m2; 人员58 或 0.37人/ m2; 设备 13W/m2; 灯光11W/m2; 水面 0.26m2 ，水温 75℃;  新风17m3/h/人集中处理, 即0.37*160*17=1006m3/h.

室内设计要求DB=25℃, RH=55%; 室外工况DB=34.8℃, WB=28.1℃; 软件计算室内负荷=17.65kW; 湿负荷=3.67kW=1.468g/s; 热湿比=12020J/g 或潜热比=20.8%; 无再热。 在室内要求附近的热湿负荷计算如表1：

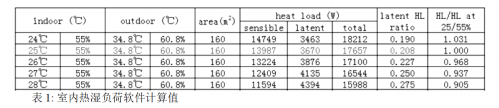
引用 i-d 向量空间语言表示上述设计，室内设计要求N=(52.89, 10.855), DB=25℃, RH=55%。室外工况W=(90.1, 21.432), DB=34.8℃, WB=28.1℃。第一与第二坐标值的单位为 kJ/kg 与 g/kg 。

新风机组φ 的送风点 K = φ (W) = (52.89, 13.212), DB =19.2℃, RH = 95%，新风处理到 iK=iN。

混风点 C = 0.262K+0.738N = (52.89, 11.473), DB=23.47℃, WB=18.64℃。

二级空调机组F的送风点 O = 热湿比12020J/g 与相对湿度 95%曲线的交点= (39.08, 9.705)。

室内负荷向量 Δ=N-O=(52.89, 10.855) - (39.08, 9.705)=(13.81, 1.15)。

风量=Q/Δi=17.65/13.81=1.278kg/s=3834m3/h；二级空调机组F的冷量=17.7kW；新风和二级空调机组的选型如图2。

前述计算可以应用焓湿图而无须应用i-d 向量空间来完成。i-d 向量空间理论关键在于热湿处理过程可直接用数学公式来表示。上述空调系统的制冷过程可以表示如下：

K = φ(W)                                        (1)

Ci = (1006K+2828Ni)/3834=0.262K+0.738Ni        (2)

Oi = F(Ci)                                        (3)

Ni+1= Oi + Δ                                        (4)

i=1,2,3……

这是一个迭代过程，当对应某i值 Ni+1 = Ni 时，则系统与室内负荷达至平衡点。公式 (1)-(4) 可组合成一个公式：对应任意室外工况W和室内负荷向量Δ，

Ni+1= F[0.262φ(W)+ 0.738Ni] + Δ           i=1,2,3……        (5)

于是上述舒适性空调系统可以用一个数学公式来表示。公式（5）中的两个变数是室外工况W和负荷向量Δ。公式（5）的意义在于对应任意室外工况W和室内负荷Δ，只要在公式内输入W和Δ，就能计算出室内空气平衡状态点。

（西交大的几位研究生曾和我争论，他们认为我所谓的理论突破是应用焓湿图就可以做计算的。比如要计算在恶劣工况40℃/70%下空调系统的性能，我只要把室外设计工况从原先的35℃/28℃改为40℃/70%即可。前几天中国建筑科学院的一位高工也如此认为。当真是这样吗？事实上在恶劣工况，他们是在设计另一个空调系统而并非计算原先在设计工况所设计的空调系统在恶劣工况下运行的参数。最后我必须搬出代表在设计工况所设计空调系统的数学公式Ni+1= F[0.262φ(W)+ 0.738Ni] + Δ，花了一个晚上的时间才能把他们说服。）

迭代过程反映出空调系统风量以及制冷量的不足，所有计算不能一步到位。同时因为经过表冷器的过程是降温除湿过程，所以所牵涉焓值和含湿量都在减小，于是迭代过程收敛。

最后，设计师给二级空调机组制冷量增加 10% 保险系数，并匹配等冷量的冷水机组，即19.5kW 。做为理论计算，不存在制造误差，所以我们选择不给空调机组增加保险系数以防止人为的数据偏差。因此二级空调机组冷量 = 17.7kW，冷水机组冷量 = 19.5kW。

新风机组φ 和二级空调机组F的选型如下：

左图左上角红色方框内的参数为新风空调机组φ的结构参数。左图为新风空调机组φ的数学模型。φ(W)=(52.79kJ/kg, 13.11g/kg) ，W=(90.1, 21.432), DB=34.8℃, WB=28.1℃。

27-12℃ 舒适性空调机组在设计工况和负荷下的运行性能参数计算

负荷向量 Δ=(13.81, 1.15)；空调机组 φ 和 F 的水流量分别为0.57l/s和0.87l/s。从图2 可得K=φ(W)= (52.79, 13.11)。 取N1=(51.81, 10.595) , DB=24.6℃, RH=55%。为了看到详细计算过程，我们使用公式 (1)-(4)来计算而不用公式(5)。

混风点C1=0.262K+0.738N1=(52.07, 11.255), DB=23.22℃, WB=18.38℃;

O1=F(C1)= (37.99, 9.45), 参考图3左图。

N2= O1+Δ= (37.99, 9.45)+ (13.81, 1.15) = (51.8, 10.6), DB=24.57℃, RH=55.1%。

N2 不等于 N1 , 所以迭代继续。

C2=0.262K+0.738N2 = (52.06, 11.259), DB=23.2℃, WB=18.38℃;

O2=F(C2)= (37.99, 9.45) =O1, 参考图3右图。

因此 N3= N2 。室内平衡空气状态点是DB=24.57℃, RH=55.1%。

二级空调机组冷量=17.73kW，所以19.5kW 的冷水机组完全能够提供7℃冷冻水。室内平衡点的干球温度和相对湿度都比设计要求稍低，原因是空调机组选型偏大。

3空调机组在恶劣工况下的性能

计算空调机组在恶劣工况下的运行性能参数，我们需要以下定律：

3.1 近等相对湿度定律

近等相对湿度定律：在给定室内负荷的前提下，在正常舒适性空调运行范围内, 提升冷冻水温或室外工况对室内相对湿度所产生的影响微小，相对湿度保持接近恒等。在特高冷冻水温度或特干室外工况等特殊情况下，室内相对湿度则不增反减。

证明：应用 i-d 向量空间理论可知, 新风集中处理空调机组的室内空气状态点

Ni+1= F[μφ(W) + (1-μ)Ni] + Δ = Oi + Δ        i=1,2,3……        (6)

μ 为新风比例, φ 与 F 为新风及二级空调机组；W 为任意室外工况；Δ为任意室内负荷向量。

对应任意常规冷冻水温度和室外工况，当表冷器处于除湿状态则二级空调机组送风状态点 Oi 将处于机械露点温度附近。于是 Oi 的相对湿度近乎恒等。

公式 (6) 是 Ni+1= Oi + Δ ，所以所剩唯一变数为 Δ 。前提是室内负荷为给定的常数，且相对湿度曲线为接近平行的曲线组，所以室内相对湿度接近相等。

若冷冻水温特高或室外工况特干，则二级空调机组的送风点比常规送风点的相对湿度更低。Ni+1= Oi + Δ 且相对湿度曲线为近平行曲线组，所以室内相对湿度也更低。

对应独立新风舒适性空调系统，计算公式为 Ni+1= F[μW+ (1-μ)Ni] + Δ 。显然这是集中新风舒适性空调系统的特例，取 φ 为恒等函数即可。

对应回风舒适性空调系统，计算公式为 Ni+1= F(Ni) 。这是集中和独立新风舒适性空调系统的特例，取μ=0即可。证毕。

表2和图表4显示回风空调机组对应7℃ 到 18℃进水温度以及一个室外极其干燥的特殊工况的送风和室内相对湿度。此空调机组的结构参数为：表冷器管径 1/2”, 排数 4, FPI 12, 孔高 12, 长度1030mm, 回路类型 0.5, 风量3726m3/h。负荷向量 Δ=(15.45, 1.545)。

表2和图4都显示当进水温度在7℃ - 12℃之间，送风状态点处于机械露点温度，相对湿度在94.2% 左右。当进水温度提升到13℃，表冷器成为干盘管，这时送风相对湿度减小而干球温度快速上升。由于 N=O+Δ而Δ为常数, 所以室内空气状态点N的相对湿度与送风点相对湿度呈相同规律。因此我们可以排除提升冷冻水温会造成室内相对湿度过高的忧虑。