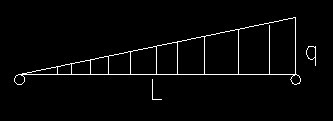
求，一两端简支梁，梁上受三角行均布荷载(见下图)，求梁上最大弯距，及最大弯距距左端距离！！
求，一两端简支梁，梁上受三角行均布荷载(见下图)，求梁上最大弯距，及最大弯距距左端距离！！
2楼
查中国建筑工业出版社的<建筑结构静力计算手册>(第二版),里面有详细的图表可查.
回复
3楼
M=三角形面积*均布的面荷载*2/3的0.5计算跨度，最大弯矩在跨中
回复
4楼
先写出该梁的弯矩方程，对它求导，该求导方程的解就是弯矩最大点，再将该点的值代入弯矩方程即可以得到结果。
回复
5楼
这个很难吗
楼主怎么拿到这儿来问阿
好好看看书吧
回复
6楼
最大弯距是在跨中吗?
回复
7楼
楼主的材料力学学得不是很好吧
这是一个静定结构的力学求解问题
用积分就可以求解
真不行就去查建筑结构静力计算手册
回复
8楼
剪力为零的位置就是弯矩最大的位置
回复
9楼
这么规则的荷载,还用会那么难算呀,距左端2/3外就是最大弯矩处了
回复
10楼
上面错了,支座反力,Fa,Fb, FaL=0.5*q*L*(L/3) Fa=qL/6
A端距最大支座为X,M=Fa*X-0.5*(q*X/L)*X*(X/3),对M求导
回复
11楼
先求两端反力，利用剪力为零求最大点。算了一下。最大点距离左端是sqrt（3）/3的位置，即1.732/3＝0.577 处
最大弯距用的求解器求得，应该是0.64。
回复
