1 、简介  

组合榫（简称 CD   ）是用于组合梁的抗剪连接件，由钢材和混凝土两部分组成（见图 1   ），取代了用于在钢材和混凝土板之间传递剪力的剪力钉。它们要么由焊接在钢梁翼缘上的钢板制成，要么通过气割直接从钢梁腹板上制成。与剪力钉相比，其主要优点是即使在高强度混凝土中也具有更高的承载能力和足够的变形能力，因此根据 EN 1994-1-1   ^[2]   ，它们可以被归类为延性抗剪连接件。此外，组合榫特别适合于采用无上翼缘型钢的组合型材，经济性也强。这样，中性轴附近的任何钢制部件都可以减到最少。另一个应用领域是在混凝土 T   梁中布置组合榫作为外部约束。然而，技术规则的缺失导致设计办公室和建筑管理局在施工过程中存在不确定性，并导致客户产生一些不情愿的想法。尽管如此，得益于技术优势，组合榫被更频繁地用于建筑以及公路和铁路桥梁。在几个欧洲国家（如德国   ^[3-5]   、奥地利   ^[6]   、波兰   ^[7,8]   、罗马尼亚   ^[9,10]   和捷克共和国   ^[11]   ），建造了大约 38   座组合材料桥梁。  

由 FOSTA —钢铁应用研究协会资助的已完成的德国研究项目 P804 ^[12] 的目的是解决有关这些创新抗剪连接件的悬而未决的问题，并为任何设计办公室或施工公司准备通用技术 准则 。 2013 年 5 月的德国通用技术 准则 Z-26.4-56 “组合榫”涵盖了回旋线（ CL ）和拼图（ PZ ）形状的组合榫（见图 1 ）。  

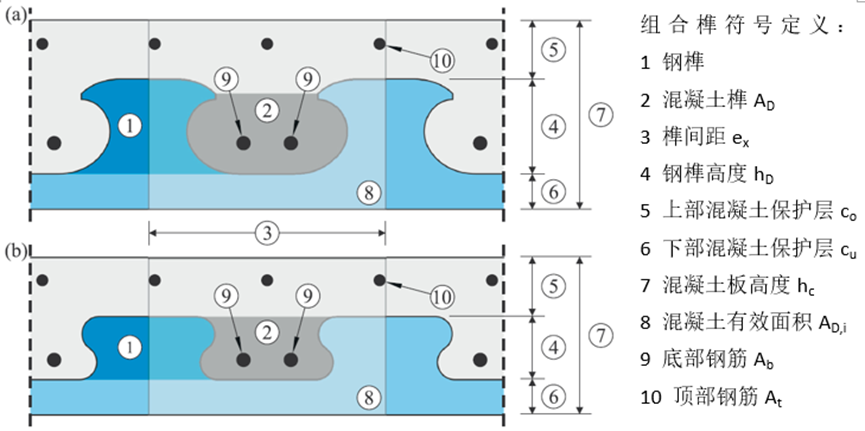
图 1   组合榫截面符号定义，（ a ）回旋线型（ b ）拼图型  

2. 现有技术  

2.1. 概述  

组合榫的发展始于 20   世纪 80   年代。起点可以追溯到 Andr?   和 Leonhardt   的研究，这导致了 Perfobond strip   的开发（见图 2   ， a   ）   ^[13,14]   。与此同时， Bode   开发了“ Kombi-Verdübelung   ”（见图 2   ， b   ）   ^[15,16]   。这些几何形状通过带孔的垂直钢板在钢梁和混凝土板之间传递剪切力。这两个设计概念都是基于混凝土部分剪切破坏的力学模型。在接下来的几年里，慕尼黑联邦国防军大学获得了关于组合榫承载性能的重要知识   ^[17,18]   。由此，获得了开口内混凝土局部面积压力超标和混凝土表面附近组合榫混凝土撬出的力学模型   ^[20,23]   。  

近年来，出现了具有拼图和回旋线形状的组合榫。 RWTH Aachen   大学的研究项目推动了具有拼图带的组合榫的开发（图 2   ， c   ）   ^[24,25,78]   。它们导致了撬出模型和新的钢板失效模型的进一步发展。 Seidl   ^[21]   开发了混凝土 T   梁中组合榫的混凝土撬出和垂直劈裂重叠效应的设计模型。回旋带使用的开端（疲劳载荷的优化）可以从参考文献 [26   ， 27]   中找到（图 2   ， b   ）。拼图型和回旋线型的几何结构都使得只需一次气割来制造两个组合榫成为可能，减少了材料的浪费甚至完全不浪费。此外，开放的几何形状可以更容易地安装钢筋，从而减少了生产成本和时间。  

参考文献 [12]   中对组合榫开发的主要步骤进行了详细描述。  

2.2 失效模型  

基于自身试验的文献和经验表明，静态载荷产生了各种失效模式。一般来说，有两种类型的破坏模式：混凝土破坏和钢破坏。在混凝土破坏领域，已知有 3   种类型（见图 3   ）。混凝土的剪切破坏可通过混凝土部分的双重剪切发生（见图 1   中的“ 2   ”）。这种失效模式对于小开口、大钢板厚度和无接缝传力钢筋 A   b （图1，“9”）   类型来说是决定性的。混凝土榫和混凝土表面（顶部或底部混凝土保护层）之间的距离较小，会导致混凝土撬出。这种破坏模式类似于混凝土在剪切力作用下从锚固件中撬出。在具有组合榫的梁型截面中，混凝土腹板的外部约束可能会失效。对于薄混凝土腹板，劈裂拉力可能超过混凝土拉应力，从而导致组合榫高度位置处出现水平裂缝（垂直劈裂）。  

除了板厚小、钢材强度低的混凝土破坏模式外，榫还可能发生钢材塑性破坏。这种失效模式是由组合剪切 -   弯曲机制引起的，该机制导致钢板出现水平裂纹。  

3 、力学模型  

使用不同的研究方法来开发力学模型，这些模型描述了组合榫的承载特性（失效模式）。根据文献中的实验结果，编制了一个数据库（第 3.1 章）。数据库分为不同的荷载类型（静态和循环），并分为混凝土（剪切、撬出）和钢（剪切）破坏模式。将参考文献 [12] 中执行的自己的测试（第 3.2 章）添加到数据库中。实验测试得到了数值模拟的支持（第 3.3 章）。  

图 2   组合榫的研制历程  

3.1   数据库

为了解决有关组合榫承载性能的悬而未决的问题，在文献研究结果的基础上建立了一个数据库。其中，仅考虑了那些无限制可重复的结果，其中失效模式是不同的（没有区块榫效应），并且所有必要的参数都记录在案。借助这些数据，可以识别组合榫发生的失效模式。其结果是，混凝土剪切的设计模型可以转换为不同的榫几何形状。因此，在自己的测试中没有对这种失效模式进行研究。另一个结果是，在静态载荷下拼图形状的榫存在大量的测试结果。由于缺乏回旋线形式相关的知识，在执行自己的测试时，这方面受到了特别的关注。  

所介绍的失效模式（第 4   章）的数据库如相关章节所示。  

3.2.   实验测试  

基于数据库中的实验测试，开发了一个测试矩阵，以便于对钢和混凝土的破坏进行调查（参见表 3-1 ）。为了开发适用于静态载荷的机械模型，根据参考文献 [2] 附录 B ，进行了六个系列的三次推出试验。为了实现各自的破坏模式，混凝土保护层、混凝土高度 hc （表 3-1 ，系列 1 和 2 ）、配筋率、混凝土 T 梁的配筋（表 3-1 、系列 3 ）和组合榫之间的横向距离 a （表 3-1 和系列 4 ）都会发生变化。为了引发明显的失效，每个系列都是根据文献中现有的设计方程预先确定尺寸的。  

表 3-1   静态载荷的实验矩阵  

系列 1 设计用于静态钢板失效（图 3 ）。为此，使用高混凝土强度等级和低钢材等级。在系列 2 中，选择尺寸和材料以实现混凝土“撬出”（向上和向下，见图 3 ）。在系列 3 中研究了组合榫和侧向混凝土保护层之间的距离（垂直劈裂，图 3 ）。因此，测试推出的试件其横截面被设计为 T 形梁。与 3.1 系列相比， 3.2 系列中设置了额外的约束箍筋，以测试其对失效的影响。在具有两个不同垂直距离的系列 4 中测试了对两个平行组合榫承载能力的影响。系列 4 中试件的尺寸（混凝土板高度、保护层和材料）与系列 2 （混凝土撬出）相同。  

在所有测试系列中，混凝土剪切通过适当的传力钢筋 A b 来防止（见图 1 ，“ 9 ”）。除了试验性的静态实验外，还进行了梁的静态和循环试验，包括回旋形和拼图形 ^[12] 。

图 3 组合榫（所示 CL 形状）因静态载荷引起的失效模式

3.3.   数值模拟    

3.3.1.   有限元模型    

为了支持实验测试，使用非线性有限元程序   ABAQUS/Explicit   进行了数值模拟，详细解释见参考文献   [48]   。钢和混凝土之间的接触被定义为法向上的“硬接触”。在切线方向上，混凝土表面和钢材表面之间的摩擦接触定义为摩擦系数μ   =0.3   。使用罚函数法对切向接触条件进行建模，该方法在动力学计算的每个步骤中都要求位移、速度和加速度之间的运动学条件的兼容性。    

“混凝土 塑性 损伤”（   CDP   ）模型用于模拟混凝土的非线性行为。这里，压缩载荷变形行为由参考文献   [28]   模拟，对于拉伸行为，选择参考文献   [29]   的应力   -   裂纹   -   张开关系。钢筋（纵向钢筋、箍筋）使用“嵌入”功能在混凝土板中实现，其中钢筋的平移自由度与相邻混凝土节点耦合。因此，在计算中忽略了混凝土和钢筋之间的任何可能滑动。通过各向同性硬化的弹塑性行为模拟钢部件。    

在下文中，将有限元研究的结果与相应的实验结果进行了比较。图   4   中的实线显示了通过试验   SD1   、   SD2   （左）和   SZ1   、   SZ2   （右）确定的力   -   位移关系，相应的数值模拟结果则是虚线   ^[48]   。尽管纵向拉伸试验（   SZ1   、   SZ2   ），纵向压缩和箍筋的参考试验（   SD1   ）的计算力   -   位移曲线可以以适当的精度进行数值模拟，但   SD2   系列（无箍筋）的试验曲线显示出额外的承载储备和比相应数值结果更具韧性的性能。    

有限元模型能够以良好的一致性模拟所有测试。除了变形和极限载荷模拟的精度满足要求之外，有限元模型还证明了裂纹模型和失效模型的精确性（图 5 ）。

图 4 有箍筋（左）和无箍筋（右）的数值模拟和试验研究的力 - 位移关系比较

图 5 有箍筋（左）和无箍筋（右）的数值模拟和试验研究的裂缝模式比较  

3.3.2.   参数研究    

有限元模型被用作进行额外参数研究的重要工具。特别是，研究了混凝土强度、板厚度和不同配筋组的影响。参数研究表明，混凝土强度的增加对抗剪承载力的影响低得不成比例，因此，混凝土强度增加   20%   至   C60/70   只会导致极限承载增加   14%   （对于受拉混凝土板）和   8%   （对于受压混凝土板）。这里，连接的延展性没有受到显著影响，并保持在与   C40/50   相同的范围内。由于混凝土板的长细比影响（   10 cm   厚），改变组合榫的埋置深度不会显著影响力   -   滑动性能或极限承载。然而，如果板的高度增加到   14cm   ，抗剪承载力将提高约   20%   。最后，研究了横向配筋度的影响。与参考试验（   SD1-SR   、   SZ1-SR   ）相比，通过安装额外箍筋来集中横向钢筋不会对剪切和变形能力产生显著影响。显然，   SD1-SR   和   SZ1-SR   中的现有箍筋似乎已经确保了混凝土榫的充分约束。    

3.3.3. 剪切传递机理分析  

组合榫钢材部分前方的混凝土楔块传递大部分剪切力。由于混凝土楔块中的三轴压缩应力状态，可以传递数倍于混凝土单轴强度的力。图 6   绘制了混凝土楔块中计算的主压应力与组合 榫 中剪切作用力的关系图。压应力是在钢拼图表面正前方的混凝土单元的积分点处进行评估的。在试验 SD1-SR   的 ABAQUS   计算中，箍筋和混凝土板受压，混凝土中的应力在超过锚固能力后达到 360 N/mm2   （见图 6   ，左）。这大约是单轴抗压强度的 9   倍。在这里，混凝土楔块受到周围混凝土、箍筋和钢榫的强烈约束，从而防止了平移，并可能发展出多轴高应力状态。另一方面，对于 SZ1-SR   ，混凝土楔块中的最大压应力仅达到约 200N/   mm ²   （单轴抗压强度的 5   倍）。混凝土板的整体纵向张力阻碍了多轴应力状态的发展。显然，在混凝土板中具有纵向张力的剪切试验中，由于约束不足，混凝土楔块在显著较低的荷载水平下破坏。图 6   （右）显示了试验 SD2-S   和 SZ2-S   的 ABAQUS   计算中混凝土楔块中的主压应力与抗剪切承载力之间的关系。在这两个试验中，主压应力约为 180 N/   mm ²   ，与纵向应力状态（压缩或拉伸）无关，其等于单轴抗压强度的 4.5   倍。当箍筋不存在时，混凝土无法获得充分约束，限制了更高的多轴应力状态的发展。    

参考文献   [60]   中给出了包括榫其他几何形状和配筋率的有限元模拟在内的进一步研究。在参考文献   [62]   中模拟了拉伸和剪切组合载荷下的特性。    

图 7 显示了参考文献 [12] 中广泛研究的非闭合箍筋混凝土屈服劈裂破坏的影响 ^[12] 。  

图 6  在有箍筋（左）和无箍筋（右）的试验中，取决于纵向应力状态（压缩 / 拉伸）的最大混凝土主压应力的发展  

图 7  （ a ）具有回旋形状的钢部件（ b ）不同的钢筋箍筋（ c ）混凝土裂缝布局的有限元结果示意  

4. 纵向静态抗剪承载力    

在下文中，将介绍在静载荷作用下组合榫的三种失效模式——钢板失效（第   4.1   节）、混凝土剪切（第   4.2   节）和混凝土撬出（第   4.3   节）。最小承载力可视为纵向特征剪切承载力   P _Rk   。根据现有的、改进的或新开发的力学模型和试验结果的统计评估，推导出三种失效模式的设计公式。不同设计概念的适用性是通过将实验值与庞大测试数据库的相应理论值进行比较来估计的。标准包括平均值校正   b _m   和变异系数   V   _δ   。通过   EN1990:2010   附录   D ^[30]   中给出的统计评估程序，显示适用性最强的力学模型被用于进一步推导设计公式。    

4.1.   钢材失效    

假设钢板厚度较小，钢材等级较低，如果组合榫钢材传递的剪切力超过塑性承载能力，则会发生钢材失效。这种失效模式是由组合剪切   -   弯曲机制引起的，该机制导致钢板出现水平裂纹。由于结构钢的韧性，这种破坏模式伴随着大的塑性变形。因此，这种失效模式是延性的。    

4.1.1.   数据库    

钢板失效力学模型的开发基于包含   60   个发生了钢板失效试验的数据库（表   4-1   ）   ^[12]   。总体而言，该数据库包括   33   个拼图形榫试验和   27   个回旋线形榫试验。为了分别建立力学模型设计公式，列出了所有确定的几何参数（见图   1   和图   8   ）、材料和试验参数（如最大载荷   P _max   和组合 榫 的变形能力δ   u   ）。    

表   4-1   “钢板失效”试验数据库   ^[12]    

4.1.2. 力学模型  

通常，临界截面包括由于弯曲而产生的剪切应力和垂直法向应力（图 8   ，右）。弯曲应力是由合力和临界截面之间的偏移引起的。剪切应力与弯曲应力之比取决于合力与临界截面之间的距离以及临界截面处的榫厚度。所有文献中的分析和半经验设计方程都是基于这个基本模型的。因此，在所有公式中，厚度 t   w   、临界截面宽度 b   _crit   和屈服强度 fy   都存在线性关系。然而，文献中的方程在临界截面的定义以及剪切和弯曲之间的相互作用方面有所不同。    

虽然参考文献 [36 ， 37] 中的模型较好地表达了拼图形状的组合榫的承载能力，但它们显然低估了回旋线形状组合榫的承载能力。由于现有模型的不足之处，参考文献 [22 ， 32] 已经研发了钢板失效模型。临界截面的确定要预先假定钢榫上的载荷 P 在高度 h _eff 内是恒定（图 8 ）。载荷 P 可分为合力 P1 （临界截面以下）和 P2 （临界截面以上）。力 P1 （见图 8 ）不会在临界截面产生应力。力 P2 的位置取决于临界截面的位置。当达到临界截面的 Mises 屈服准则时，即达到承载能力。假设应力塑性分布。当承载能力达到最小值时，就可定义为临界截面。

式中    

图 8   钢板失效模式示意图  

图 9 显示了进一步研发的模型的统计评估和灵敏度分析结果。特别是对于回旋形组合榫的试验，新模型提供了更好的结果。试验中的载荷较高，且往往高于设计方程计算的载荷，一方面可以用材料超过设计强度来解释，另一方面，在回旋形的情况下，下一个混凝土榫的支撑作用减少了弯曲。  

图 9  根据文献 [12] ，对钢板失效的力学模型进行敏感性分析和统计评估  

基于该力学模型，忽略任何材料超过设计强度情况下的特征承载能力由方程式 2   表示。方程式考虑了屈服强度 fy   、传力杆的厚度 t   w   和临界截面的宽度 b   _crit   。    

基于该力学模型，忽略任何材料超过设计强度情况下的特征承载能力由方程式 2 表示。方程式考虑了屈服强度 fy 、传力杆的厚度 tw 和临界截面的宽度 b _crit 。  

由于回旋线（ CL ）和拼图形（ PZ ）组合榫的几何形状是可缩放的，所有几何参数都可以根据榫间距 e x 来表示。这些几何形状的设计方程如下：  

4.2   混凝土剪切破坏    

特别是对于榫和大钢板之间的小孔，主要的破坏模式是混凝土榫的双平面剪切。因此，承载能力的主要参数是混凝土榫的剪切面积   A _D   和混凝土的抗剪强度。因此，由于横向布置的钢筋的附加锚固作用，计算承载能力时，位于开口中的横向钢筋的影响是非常重要的因素。在大开口中，两个剪切平面合并，这由几何相关的折减系数η   _D   来考虑。对于有足够大的开口（由一般技术准则的应用范围保证），混凝土剪切被视为一种延性破坏模式。    

4.2.1.   数据库    

基于参考文献 [19,33] 中的 13 个试验数据库（表 4-2 ），开发了混凝土剪切的力学模型。列出了所有确定的几何形状、材料和试验参数，以导出设计公式。  

表   4-2   破坏模式为“混凝土剪切”的试验数据库   ^[12]    

4.2.2   力学模型    

混凝土剪切的特点是混凝土榫的双平面剪切破坏（见图 10 ）。可以在 [14 ， 16 ， 19 ， 21 ， 37]这些文献 中找到几个设计方程。所有方程分别考虑剪切面积 A _D 和混凝土抗压强度 f _c 和抗拉强度 f _ct 。此外，参考文献 [19] 中考虑了钢榫高度 h _D 、文献 [37] 考虑了厚度 t _w 以及文献 [21] 考虑了钢筋直径以及钢筋的屈服强度 f _S 。  

图 10  混凝土剪切的示意图，以及 A _D 定义 （ a ）回旋线形 （ b ）拼图形  

文献中的所有设计公式都与试验中的承载能力相吻合。然而，参考文献 [16] 中的公式适用性太低。与其他模型相比，参考文献 [19] 的模型计算结果波动性最小。此外，该模型很好地考虑了混凝土抗压强度和大型混凝土 榫 剪切面积减少的影响。因此，基于参考文献 [19] 的方法，导出了一个设计方程。为了与混凝土撬出模型（第 4.3.2 章）一致，使用了混凝土抗拉强度和混凝土抗压强度之间的关系（ f _ct ~f _c ^0.5 ）以及参考文献 [31] 定义的配筋率。最终，考虑混凝土抗压强度 fck 、剪切面积 A _D 、钢榫高度 h _D 和配筋率ρ _D ，计算了混凝土抗剪强度。

式中

系数   16.542   是对   1.00   的平均值修正，也包括了剪切平面的数量以及混凝土抗压强度和抗剪强度的关系。    

由于剪切面积 A _D 与 (e _x ) ² （回旋线形状： A _D =0.198 (e _x ) ² ；拼图形状 A _D =0.133 (e _x ) ² ）以及 h _D 与 e _x （回旋线形： h _D =0.400 e _x ；拼图形状 h _D =0.267 e _x ）的函数关系，方程 5 可以简化如下：

式中    

（回旋线形状）

（拼图形状）    

最后，值得注意的是，在通常情况下，具有技术准则中给出的几何形状的组合榫不会发生混凝土剪切。因此，这种失效模式几乎没有实际意义。

4.3. 混凝土撬出  

混凝土榫和混凝土表面之间的距离（顶部混凝土保护层 c o 或底部混凝土保护层 c u ）较小，可能会引发类似于混凝土在剪切力作用下从锚固件中撬出的破坏模式。荷载加载区域的静载压力会产生横向张力，这会导致（在混凝土保护层不足的情况下）锥形混凝土撬出（图 11 ， a ）。撬出可能发生在混凝土顶面或底部，具体取决于钢筋在混凝土中的位置。混凝土撬出同时也会造成榫的静压力损失，从而导致二次混凝土压力失效。这种破坏模式被认为是延性的。  

图 11 （ a ）潜在撬出锥体的示意图，（ b ）纵向重叠撬出锥体（ c ）横向重叠撬出锥体  

4.3.1. 数据库  

失效模式为混凝土撬出的数据库共包含 77 项测试，包括 20 项拼图形状榫测试和 3 项回旋形榫测试（参见表 3-1 ，系列 2 ）。此外，该数据库还包括锯齿形、 Kombi-Verdübelung （ K ）、开放式 Kombi-Veldübelung （开放式 K ）、椭圆形和斜角开放式 Kompi-Verdúbelong （ aK- 开放式）的测试，这些测试都发生了混凝土撬出破坏。所有确定的几何形状、材料和试验参数都被列出，见表 4-3 。  

表   4-3   失效模式为“混凝土撬出”的试验数据库   ^[12]    

4.3.2 力学模型  

在文献   [19   ，   21   ，   31]   中，有三种混凝土撬出模型，它们确定了混凝土抗拉强度和撬出锥体表面积的撬出阻力。在每种情况下，撬出锥体的壳体表面由锥体的高度   h _po   决定（图   11   ，   a   ）。此外，文献   [21]   引入了折减系数χ   _x   和χ   _y   ，其中考虑了榫在纵向方向上的间距   e _x   （图   11   ，   b   ）和两个组合榫之间的横向距离   e _y   （图   11   、   c   ）。此外，文献   [19   ，   31]   还额外考虑了横向钢筋配筋率ρ。    

为了推导设计方程，选择了参考文献 [31] 中的精确力学模型，得出了一个简单的公式。如上所述，通过引入系数χ _x 和χ _y ，考虑到组合榫的承载能力受到间距 e _x 和 e _y 的影响。这些因素在文献 [21] 中有详细推导，如果 榫 布置得很近，还考虑了混凝土撬锥的重叠面积（见图 8 （ b ）和（ c ））。常数值 40.44 是通过实验确定的经验因子。它涵盖了混凝土抗剪承载力与混凝土抗压强度的关系，以及撬出锥体面积与锥体高度 h _po 的关系。  

式中

χ因子对补充模型的统计评估和敏感性分析结果如图 12 所示。新模型特别适用于回旋形榫测试和拼图形榫测试，提供了更好的结果。综合所有测试结果，新模型实现了良好的平均值校正（ b _m =0.97 ）和轻微波动（变异系数 V _δ =0.13 ）。  

图 12 根据文献 [12] ，混凝土撬出力学模型的敏感性分析和统计评估  

为了简化设计方程（等式 7 ），η被一个常数值代替，该常数值是文献 [2] 根据混凝土的最低强度等级为 C20/25 确定的。此外，局部安全系数 γ _V =1.25 ，校正系数为 0.82 。混凝土撬出的简化设计方程如下：  

翻译：张贤卿

编辑：张贤卿

审核：王昌将