上世纪40年代，塔科马大桥风毁事件使得桥梁抗风稳定性研究逐渐发展起来。而在历史上，人行桥因风致振动而发生破坏的例子也是屡见不鲜。苏格兰的德莱堡修道院大桥于1817年建成，在建成后的第二年就因风致振动使得其部分桥索发生破坏，随后被一场大风彻底摧毁。位于美国西弗吉尼亚州的惠灵大桥于1854年5月被一场大风掀翻桥面，英格兰的布莱顿栈桥于1896年发生风致破坏。早些年，人行悬索桥的跨径一般在300米以下，其抗风稳定性问题并没有得到足够的重视。如今，随着技术的不断发展以及各种地形的要求，人行悬索桥的跨径已经突破500米，使我们必须要面临一系列新的风致振动问题，尤其是大跨径人行悬索桥的颤振稳定性问题。人行悬索桥跨径不断增大，而主梁的宽度和高度均较小，结构更加轻柔，这使其频率相对较小，相较于公路桥更容易产生大的振动和变形。而且人行悬索桥还有桥面构造简单、设计寿命相对较短等特点，这与公路桥明显不同。因此直接使用公路桥梁规范对其进行抗风设计具有不合理性，在抗风设计中需要采取相应的措施，来应对大跨径悬索桥所面临的风致振动问题。

目前国内尚无较完善的专为人行桥编制的规范，现行《城市人行天桥与人行地道技术规范》由于发行时间较早，很多条例已不再适用于现在复杂多变的人群以及其他外界环境的作用，而且也仅仅适用于城市人行天桥，对其他类型的人行桥，诸如景区人行桥、跨河人行桥也未做专门说明。近年来，经济的高速发展及建筑结构的泛娱乐化倾向，使得玻璃人行桥等特殊桥梁得以迅速发展，但是暂未形成完整与成熟的设计方法，这也成为新兴桥型进一步推广发展的阻碍。

在桥梁的抗风设计中，需保证结构自身所能承受的临界风速高于桥址位置的检验风速。对于平坦地区，国内普遍采用指数律风剖面（公式1）计算设计基准风速。

U(z)=U₁₀ (Z/10)^α　　公式1

其中U10表示基本风速，α为地表粗糙度系数，z为结构或构件的基准高度。现行抗风规范将地区按其表面粗糙度划分为四类场地，相应的风剖面随高度变化规律如图1所示。需通过结构位置与桥下地面或水面的相对高度来确定实际基准高度，并根据桥址处的地表场地类型，选择地表粗糙度系数。

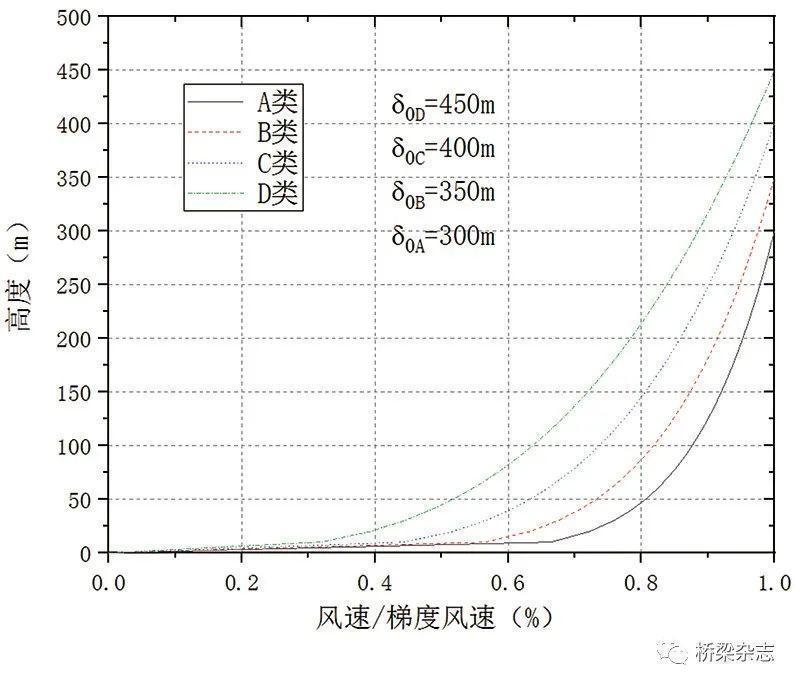
图1 四类场地风剖面

大跨径人行悬索桥主要位于景区内部，多数要跨越山谷，因而桥面位置距谷底距离很大，且沿桥跨方向存在明显变化。地表剧烈的起伏变化使得山谷地区风场与平坦地区的良态风有很大区别，如若继续采用规范方法设计基准风速的计算会存在以下两个主要问题：首先，选取何处地表作为参考位置来计算基准高度存在不确定性。如选取谷底最低位置，则会因过于保守而使得颤振检验风速过大，从而大幅提高桥梁造价以及抗风设计难度。此外，山谷地区地表粗糙度变化更为明显，确定更为合理的地表粗糙度系数也是需进一步研究的问题。

对于特殊地形下的风场特性研究，一般采取三种措施，即现场实测、风洞地形模型试验、计算流体力学模拟（CFD）。以两个典型山谷地形桥址为例，通过实测数据与规范风剖面进行对比，对山谷地区的风场特性进行研究。

Y形汇流谷

大董路特大桥地处Y形汇流谷，如图2。

图2 大董路特大桥效果图

在桥址处安装观测设备，采集风场数据，得到实测数据与规范风剖面进行对比。通过对比可以发现，在近地表范围内，实测平均风速并没有因地表粗糙度的影响而产生明显的减小，在低空区用规范所提出的方法计算将低估平均风速，而在高空区则高估了平均风速。高空区的风速高估会对桥梁抗风设计增加不必要的困难，并会因此提高桥梁造价。而低空区的风速低估则会使得桥梁设计存在潜在危险性。

喇叭口收缩谷

禹门口大桥桥址处地形为喇叭口收缩谷，其效果图如图3，在桥址附近建立观测站来监测当地风场特性。

图3 禹门口大桥效果图

将实测数据与规范中D类场地规范计算值进行对比。结果表明，在距地面高度100米以上的实测平均风速要低于规范计算值，而在100米以下实测平均风速则明显高于计算值。该地区同样存在低空区平均风速被低估，高空区平均风速被高估的情况，且实测值与规范计算值对比更加明显。

人行悬索桥风致振动主要形式

对于大跨人行悬索桥，抗风稳定性问题主要是颤振、涡振以及静风失稳。其中最值得注意的是人行悬索桥的颤振问题。历史上，绝大多数的人行桥风毁事件均是由于颤振导致。由于人行悬索桥的气动稳定性差，所以往往颤振临界风速较低，在不进行优化的情况下一般很难满足抗风稳定性要求。

龙潭大峡谷玻璃吊桥是一座人行大跨悬索玻璃桥，近年来这种富有观赏性的桥型愈发增多。而在对其进行风洞抗振试验研究时，发现该桥在较低风速下便会发生明显颤振。即使实际桥梁不会在该风速下因颤振而毁坏，也势必会降低其抗风稳定性。如不尽早加以合理的防范，结构很可能因一次次的振动而最终发生破坏。此外贵州某人行悬索桥也因自身稳定性问题在低风速下发生大幅振动。该桥在风力作用下发生明显侧弯、竖弯及扭转振动，振幅巨大，且随着风速的增加呈现发散趋势。上述实例也进一步说明，大跨径人行悬索桥的颤振问题需要高度重视。

涡振问题因近年来的多发性而逐渐受到关注，如西侯门大桥、伏尔加河大桥，都曾因涡振问题而成为焦点。涡振一般为低风速和固定频率区段内发生的限幅振动，会影响桥面的行车舒适度，并对结构产生一定的疲劳破坏。涡振振幅控制主要以保证行车安全以及舒适度为目的。对于涡振的发生，一般要同时满足三个条件。首先，结构自身的阻尼比很低，低阻尼会使结构更容易发生风致振动。其二，桥梁断面的气动特性差，风致振动普遍对桥梁截面形式比较敏感，因而桥梁断面的气动性差也是涡振发生的必备条件。第三，需特定气象条件，这涉及来流风向角以及风速等多方面问题。

上述桥梁均为公路桥梁，对人行悬索桥而言，涡振问题便没有那么突出。首先，由于人行桥主梁结构更为简单，且一般通透性好，所以不易发生涡振。另一方面，人行桥不会因视距等原因而对行人安全产生明显影响。对于某些景区内桥梁，出于对其娱乐性的考虑，还需桥梁产生一定的小幅振动以增加旅游乐趣。总体而言，大跨人行悬索桥的涡振问题不算严重，而且对振幅也可适当放宽，因此在人行悬索桥的抗风设计中一般并不考虑其涡振稳定性问题。

另一个需要关注的是人行悬索桥的静风稳定性问题。对于一般的桥梁，静风失稳风速远高于颤振临界风速，所以在以往的桥梁抗风设计中不会过多关注静风稳定性问题。但对于大跨人行悬索桥这种轻柔的桥型，静风失稳风速很可能会低于动力失稳风速，成为桥梁抗风设计的主控因素。在同济大学对汕头海峡二桥进行风洞试验的过程中出现了突发的静力失稳，使得模型在很短时间内破坏。而失稳时的风速远低于静风稳定理论的计算值，并且也低于该桥的动力失稳风速。这说明随着桥型的不断变化以及桥梁跨径的不断增加，已经存在静力失稳风速低于颤振临界风速的情况。尤其是更加轻柔的桥型，在设计过程中更需重视其静风失稳问题。同样，在对天蒙景区人行悬索桥的数值模拟分析中，也出现了明显的静风扭转失稳现象。图4为天蒙人行桥的效果图，数值模拟中跨中静风位移。可以看到跨中扭转位移在80m/s时发生突变，结构刚度失效，发生明显静风扭转失稳现象。即便该失稳现象不会直接导致桥梁结构毁坏，但由于其突发性，且极为迅速，巨大的位移变化会造成行人的伤亡。

图4 天蒙人行桥效果图

人行悬索桥风振控制措施

在桥梁抗风设计中，可采取各种措施提高桥梁的抗风稳定性，主要包括结构措施、气动措施、机械措施。其中，加设中央扣、辅助锁等结构措施可增加结构的总体刚度。设计开敞式桥面，增设适当的风嘴、中央稳定板、导流板、对拉索进行表面加工等气动措施，能改善桥梁结构表面流场特性。通过外加TMD或TLD等阻尼器可增加附加阻尼，以提高结构的气动稳定性或降低风振响应。

气动措施一般为对主梁的断面形式以及附属构件进行改进和优化，以提高桥梁的风致振动稳定性，图5为桥梁抗风气动措施在实桥上的实际应用。

图5 实桥气动措施

图6 孝心桥效果图

图6为四川孝心桥效果图，该桥矢跨比很小，原始方案既不满足涡振稳定性要求，也不满足颤振稳定性要求。该桥没有采用结构措施或机械措施，而是通过多个不同的方式封闭栏杆，改变主梁附近的流场形式，以提高结构的抗风稳定性。值得一提的是，气动措施并不是受力构件，而是通过改变来流的路径来改善截面的气动特性。因此在实际使用中，气动措施在满足刚度的前提下，可以选择轻质通透的材料，以提高桥梁的观赏性。对之前提及的天蒙景区人行悬索桥，也同样使用封锁护栏提高结构的颤振稳定性。

图7 合川桥效果图

图7为重庆合川渠江景观大桥效果图，该桥梁半幅用以行车，另外半幅为混合交通。该桥也同时存在颤振和涡振的问题；涡振问题为主。该桥梁采用多种混合气动措施提高结构稳定性，优化方案一为设置风嘴，封闭栏杆并封闭检修道；优化方案二为修改人行道加封闭检修车轨道槽口。两个优化方案的实验结果如表1所示，表明两个优化措施均能消除该桥梁的涡振现象，并提高其颤振临界风速使之满足颤振稳定性要求。

另一个常用的风振控制措施，是通过外加阻尼器提高结构的稳定性。结构随着自身阻尼的增大，起振可能性减小，且振动后衰减加快。阻尼器的种类繁多，按是否调谐分为调谐式阻尼器和非调谐式阻尼器。其中调谐式阻尼器主要包括TMD、TLD以及TLCD，非调谐式阻尼器主要包括黏性剪切型阻尼器、油阻尼器、高阻尼橡胶阻尼器。按外界能量是否输入又分为主动控制型、被动控制型和半主动控制型，主动控制型阻尼器需要施加外部能量，并由激励器直接实时控制；被动控制型阻尼器不需输入外部能量；半主动控制型阻尼器为通过输入能量，控制被动控制的刚度、阻尼等动力参数，适应被控体动力特性变化。

许多桥梁的颤振对结构阻尼并不敏感，结构阻尼的大小并不会对其颤振临界风速产生明显影响，决定桥梁结构颤振性能的主要是其气动外形。而对于涡振来说，结构阻尼、气动外形以及气候条件均有显著影响，因此阻尼器一般用以控制涡振的发生。图8为英国伦敦泰晤士河上的千禧桥，该桥为扁平人行悬索桥。在风致作用下产生大幅的静风位移，通过外加阻尼器来加以控制。制振措施包括由7种共计37个黏滞阻尼器提供侧向阻尼，并在跨中多加四对侧向TMD（2.5t），再由26对竖向TMD（1～3t）提供竖向阻尼。同样对于合川渠江景观大桥也通过施加一系列的TMD来提高其涡振稳定性。

图8 英国千禧桥

对于颤振现象，无论是公路桥还是人行桥都需要高度重视，而对于涡振，公路桥和人行桥则有着不同的关注点。基于之前的探讨和分析，就人行悬索桥的风致振动问题可以得到如下结论：

1.人行悬索桥的涡振问题

对人行悬索桥来说，其涡振问题并不严重。首先，由于人行桥主梁结构更加简单，通透性好，所以使得结构表面旋涡的能量不容易集中，从而提高结构涡振稳定性。且大跨径的人行悬索桥一般位于山区，受地形影响，桥址处的风场紊流度会更大。根据现有研究，桥梁结构的涡振振幅会随着紊流度的提高而降低，因此山区桥梁发生涡振的可能性更低。同时，山区复杂的地形会使主梁沿跨径方向的风场均一性变差，非均匀的风速及风攻角分布也能够降低结构的涡振概率。

目前，人行桥对涡振振幅标准还没有明确规定，一般会参照公路桥的相应规范进行设计。涡振振幅的接受程度主要取决于行车或行人的舒适度，对于舒适度的评价因人而异，在公路桥梁抗风规范中，以主梁振动加速度作为衡量因素。现行公路桥梁抗风规范中以1m/s^2的振动加速度为判定标准，以此计算主梁的竖向和扭转最大振幅。而对人行桥来说，行人在过桥时的体感与行车有很大不同，因而对舒适度的要求也会不同，再直接使用公路规范的限定幅值是不合适的。此处推荐以0.3 m/s^2的加速度为标准，并采用规范公式来计算人行悬索桥的涡振最大振幅。

2.人行悬索桥的颤振问题

桥梁的颤振要求结构自身的颤振临界风速要高于桥址处的颤振检验风速。

U_f >γ_fγ_tγ_aU_d　　公式2

公式2为公路桥梁的颤振临界风速计算公式，式中U_d表示桥梁或构件的设计基准风速；γ_f表示颤振稳定性分项系数，根据获取颤振临界风速的方法确定；γ_t表示风速脉动空间影响分项系数，由桥址处地表场地类型以及桥梁跨径确定；γ_a表示攻角效应分项系数，体现大攻角的影响。现行的桥梁抗风规范并没有对人行桥的颤振临界风速计算方式进行专门的制定，因此也使用该公式进行相应的计算。鉴于人行桥的使用寿命远低于公路桥梁，因此其所需的颤振风速可能会明显低于该计算值。

虽然在前文中提到我们需要高度重视人行悬索桥的颤振问题，但总体来看，人行悬索桥的颤振威胁要小于公路桥。一方面，人行桥通行要求低于公路桥梁，且许多属非必要通道，所以在高风速时段可以迅速地组织封桥，能有效避免桥梁颤振所带来的人员伤亡。另一方面，人行桥结构更加轻柔，相比于公路桥能承受更大的变形，因而也更不容易被风致振动所破坏，所以人行悬索桥的颤振威胁小于公路桥梁。

内容源于网络，旨在分享，如有侵权，请联系删除

相关资料推荐：

人行悬索桥设计

https://ziliao.co188.com/d44112030.html

知识点：聚焦人行悬索桥的抗风特殊性