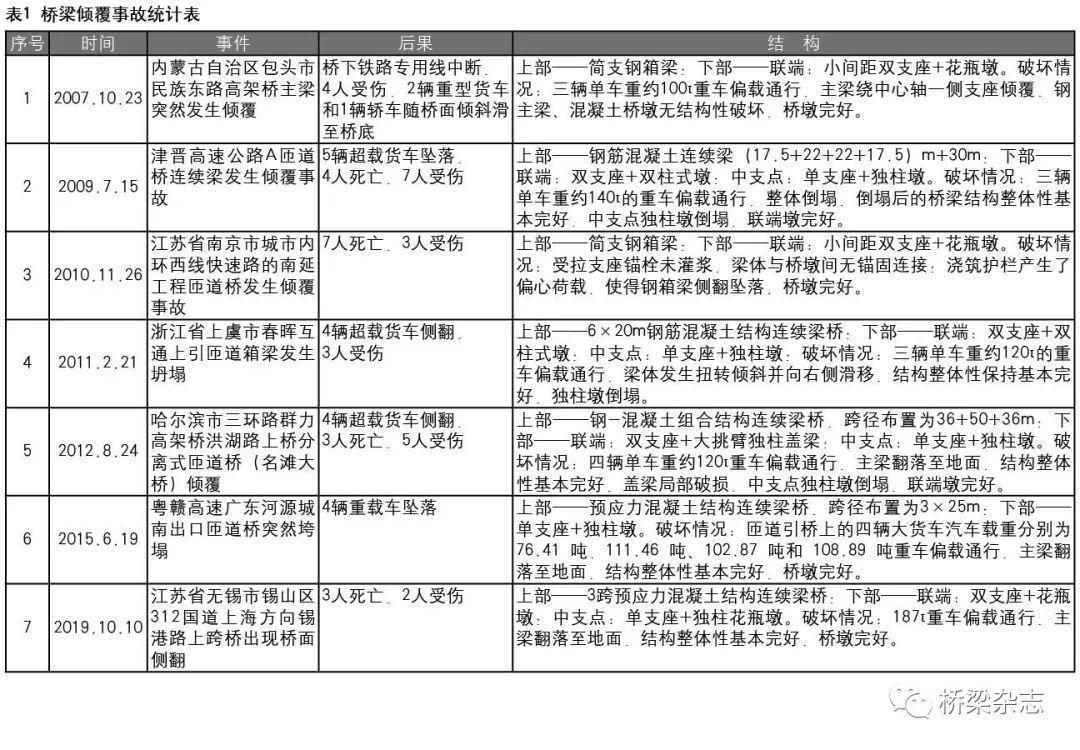
近些年来，桥梁倾覆事故屡有发生（表1，图1-图7），造成了严重的人员伤亡、经济损失和社会影响。在发生倾覆事故的桥梁中，独柱墩且横向单支点结构占有相当的比例。于是，人们对这种结构自然会产生各种各样的看法。一种观点认为，这种结构完全不能使用，对既有的这种结构必须全部进行加固或替换。另一种观点认为，既然超载是造成倾覆事故的主因，那么就跟独柱墩单支点问题完全无关。第三种观点认为，尽管超载是造成倾覆事故的元凶，也不可能按照超载的需求去设计桥梁，但从技术角度，仍需进一步提高对桥梁倾覆问题的认识，对倾覆的机理进行更细致和清楚的分析，提高桥梁的抗倾覆能力。本文作者持最后这种观点。实际上，目前对桥梁倾覆的机理和分析方法也存在不同的认识，有些认识甚至是相悖的。例如，曲线梁桥与直线梁桥相比，抗倾覆性是更好还是更差？又如，《公路钢筋混凝土及预应力混凝土桥涵设计规范JTG 3362—2018》（以下简称2018新规范）中给出的抗倾覆验算方法是否存在不足？这也表明，对此问题给予充分认识和继续努力研究是十分必要的。

本文拟简述一下梁桥倾覆的基本机理，简要分析直线与曲线桥的抗倾覆能力，并对2018新规范抗倾覆验算方法提出简略的改进建议。

图1 2007年内蒙古包头高架桥侧翻

（引自新华网）

图2 2009年津晋高速倾覆

（引自新华网）

图3  2010年南京高架桥倾覆事故

（引自新华网）

图4  2011年浙江上虞立交桥坍塌事故

（引自新华网）

图5 2012年哈尔滨三环路群力高架桥坍塌

（引自新华网）

图6  2015年粤赣高速匝道断裂坍塌事故

（引自互联网参考消息）

图7 2019年江苏无锡高架侧翻事故

（引自互联网www.zjlq.net）

通过对前述各事故桥梁的分析，发现这些倾覆事故具有如下特点——梁部整体倾覆（翻落、滑落），梁体和墩台本身无结构性破坏，或倾覆过程中，由于梁体的倾斜致使独柱墩倾斜或倒塌，进而引起梁体完全倾覆。没有因梁体本身强度不足而产生的扭断或弯断、墩台强度或稳定性不足首先倒塌或严重倾覆而导致的垮塌等现象。

根据以上特点，结合结构受力特征分析，并参考已发表的一些文献，可大体对其倾覆机理描述如下——梁体结构在偏载作用下发生弯曲和扭转变形，导致支座反力重分配。当偏载加大到一定程度时，远离倾覆轴的单向受压支座逐渐脱空，结构约束体系发生变化，梁体绕倾覆轴线转动。随着偏载继续增加，梁体的转动继续加大，转动角到达一定程度时，梁体开始侧向滑移，引发桥梁倾覆。此过程中，可能还因梁体转动倾斜而产生对独柱墩的侧向作用力，使独柱墩发生大的侧向变形甚至破坏，从而加快梁体的倾覆。

在上述倾覆发生的过程中，梁体运动始终是结构变形和刚体运动的结合模式，只不过在支座脱空前，结构变形导致的位移占主要成分。支座脱空后，刚体运动逐渐占主要成分。但不管二者谁占主要成分，最终发生倾覆都是梁体整个翻落或滑落。因此，从梁体的平衡关系入手，寻求合理的计算分析方法是可行的。值得注意的是，这里的平衡关系中，支座反力和荷载力矩必须按照结构受力状态取值，也就是说，要考虑结构变形、约束体系改变、梁横截面扭转中心与支承点不重合等，对支座反力和结构受力的影响。如果要作更精确的过程分析，还须考虑结构变形和运动对荷载的非线性影响。注意，并非只有扭转变形才影响倾覆，弯曲变形也影响支座反力重分布，而且在弯梁桥中，弯扭本来就是耦合的。无论采用简化的设计计算方法，还是复杂的有限元空间分析方法，都应在充分理解倾覆机理和结构破坏过程的基础上，建立正确的数学模型来实施计算，否则就会得出不正确的结果。

另一个值得注意的问题是，进行抗倾覆分析时，不能仅仅考虑梁的每个横截面内的受力关系，而是要把整个梁体作为一个空间的弹性体来考虑其倾覆运动。这个问题说起来很简单，但却容易被忽略，后面关于曲线桥的讨论还会涉及此问题。

对于曲线梁桥的抗倾覆能力是否优于直线梁桥，目前尚存在两种截然相反的看法，一种认为比直线梁桥差，一种认为比直线梁桥好。当然这种比较是在二者除曲率外，其他条件相同的情况下进行的。

第一种意见主要是受2018新规范计算方法的影响，认为按照新规范（4.1.8条）计算会得出曲线桥抗倾覆能力不如直线桥的结论。实际上，我们从最简单的受力机理入手，很容易得出相反的结论，即曲线梁桥抗倾覆能力大于直线梁桥，且曲率半径越小，抗倾覆能力越大。

首先，定性地分析一下。如图8和图9所示，图中阴影部分为车辆作用不利区域，即产生倾覆力矩的区域而非阴影区域为产生稳定力矩的区域。很明显，曲线梁桥稳定力矩（空白区域重量乘以其重心到倾覆轴距离）大于相同跨径布置的直线梁桥。

图8 直线梁桥倾覆轴线示意图

图9 曲线梁桥倾覆轴线示意图

接着我们分析一下2018新规范的验算方法。新规范4.1.8条——

4.1.8 持久状况下，梁桥不应发生结构体系改变，并应同时满足下列规定。

1 在作用基本组合下，单向受压支座始终保持受压状态。

2 按作用标准值进行组合时（按本规范第7.1.1条取用），整体式截面简支梁和连续梁的作用效应应符合下式要求：

式中：k_qf—横向抗倾覆稳定性系数，取k_qf=2.5；

∑S_bk,i— 使上部结构稳定的效应设计值；

∑S_sk,i —使上部结构失稳的效应设计值。

如果对于k_qf=2.5是否合适暂且不论，单从形式上看，这条规定并无不妥。问题出在规范对公式4.1.8的条文解释上，即对其中的稳定效应和失稳效应如何计算的解释上。在该规范条文解释中，稳定效应和失稳效应的计算方法为：先按全部支座有效分别计算稳定荷载和失稳荷载产生的支反力，然后在每一个支承截面处，按两种荷载对应的反力分别对不会脱空的那个支座取矩，把各个支承截面处的该两种荷载对应的力矩分别求和，就得到公式4.1.8中的稳定效应和失稳效应。

仔细分析这种计算方法，不难发现其存在两个问题。第一，把各个支承截面处的该两种荷载对应的力矩分别求和时，力矩矢量都是平行于梁轴线切线方向的。因此对于直线桥，梁轴线为直线，力矩矢量方向都相同。但对于曲线桥，梁轴线为曲线，力矩矢量方向是处处变化的。第二，各力矩是相对于不同的轴线取矩的。因此，把不同方向且对不同轴线的力矩直接进行标量求和，所得结果没有确切的力学意义。这也是为什么按此计算会得到曲线桥抗倾覆性好于直线桥的结论的原因所在。实际上，即使粗略地按照荷载及反力对倾覆轴取矩进行计算，也能得出大致合理的结论。规范该条文的出发点是放弃倾覆轴概念，采用倾覆极限状态概念，这本无问题。较早的倾覆轴概念简单地把梁体当作刚体对待，这是有缺陷的。如本文前面所述，实际的倾覆是变形与刚体耦合运动的结果。但规范条文说明的力学模型及原理却显得有些不够清楚，所得结果也不尽合理。

关于改进意见，其实并不需要对规范正文的公式4.1.8进行修改，而只修改条文说明中的内容就可以得到正确的方法，即把对稳定效应和失稳效应计算的方法说明，重新正确描述即可。当然具体如何描述还需要根据前面的分析与原则，综合考虑上下部结构及大转动角效应，通过详细的计算分析方能得出，本文不拟详述。但须注意，计算应分别采用车道荷载和车辆荷载进行，取最不利工况。

通过上述分析，我们不难得出对此问题的如下结论——

（1）已发生的桥梁倾覆事故中，超载是主因，结构形式不是控制因素。因此，并不需要对独柱墩单支点桥梁全部进行加固或改造。

（2）鉴于独柱墩单支点桥梁的特点，宜对这种结构（尤其是直线桥和相对大曲率半径桥）进行具体分析，并注意采用正确合理的分析方法，对不符合要求的桥梁进行加固或改造。