桥渡设计是一门基础科学与工程技术之间的交叉学科，涵盖了桥梁学、水文学、水文地理学、水力学、数理统计学等多个学科的知识，水力学原理在桥渡设计中的应用尤为重要。

在桥渡设计中水流状态的判断是一个基本且重要的环节，缓流和急流的区分不仅影响桥梁的结构设计，还关系到桥梁的整体安全性。通过临界流速、临界水深以及弗劳德数等水力学指标，可以准确判断水流状态，为桥梁设计提供理论支撑。

此外，桥涵结构参数的确定也需要充分运用水力学原理。桥孔的尺寸和数量直接影响水流的通过能力和桥梁的整体稳定性。通过应用恒定流连续方程和谢才-曼宁公式，可以科学确定桥孔的合理尺寸和布置方式，确保在极端水文条件下桥梁的安全运行。

综上所述，《桥渡设计》是水力学基本原理与实际桥梁工程的结合，《水力学》课程是《桥渡设计》的前导课程。但由于两课程间隔时间较长，学生对水力学的部分知识点存在遗忘现象，加之《桥渡设计》课程中对已经学过的水力学原理基本是点到为止、一带而过，这导致不少学生只知其然，而不知其所以然。本文对《桥渡设计》课程中涉及到的典型水力现象和原理进行总结回顾，以期对学生的课程学习有所裨益。

1 水力学基本概念

1.1 恒定流与非恒定流

在流体力学中，恒定流和非恒定流是两种基本的流动状态，主要区别在于流动参数随时间的变化情况。

恒定流指的是流场中各空间点上的一切运动要素都不随时间变化的流动，即恒定流中一切运动要素（如流速、压强和密度等）只是空间坐标的函数，而与时间t无关。例如，当水箱中的水位保持不变时，则出水管水流属于恒定流。

非恒定流是指流体的运动要素在空间和时间上均随时间变化的流动状态。非恒定流广泛存在于各种自然现象和工程问题中，如潮汐流动、水泵启动和停止过程中的流动变化、气象变化等。在实际工程中，不少非恒定流问题的运动要素随时间变化非常缓慢，则可近似地将其作为恒定流来处理。

1.2 均匀流与非均匀流

均匀流与非均匀流的主要区别在于位于同一流线上各质点的流速矢量是否沿着流程变化。

均匀流是指流体的流动参数（如速度、压力、密度等）在空间上不随位置变化的流动状态。均匀流的流线为互相平行的直线，这种流动状态下的流体只有沿程损失，而没有局部损失。均匀流的过水断面为平面，各过流断面上的流速分布沿程不变。

非均匀流是指流体的流动参数在空间上随位置发生变化的流动状态。根据流线沿程变化的缓急程度，非均匀流可以分为渐变流和急变流。渐变流是指各流线接近平行直线的流动状态，其流线之间的夹角很小，流线的曲率半径很大；相反，若流线的变化较为剧烈，则称为急变流。在实际工程中，非均匀流现象广泛存在。比如河道过水断面沿程发生变化、河畔修建建筑物、沿程有流量汇入或分出，以及沿程底坡发生变化等，都会导致水流发生非均匀流动。

1.3 层流与紊流

层流和紊流对应于水流的两种不同流动状态，他们具有不同的特点、形成条件和应用场景。

层流是流体在管道或明渠中以平行层的形式流动，各层之间几乎没有混合。层流通常发生在流速较低和黏性较大的条件下，流体质点沿着固定的路径运动，互不干扰。层流的一个典型特征是其流动呈现出稳定、光滑的流线。

紊流是指流体流速达到一定程度后出现的复杂流动状态。在紊流中，流体质点进行无规则运动，相互混合，运动轨迹曲折且混乱。紊流具有以下主要特征：无序性、耗能性和扩散性。首先，紊流中的流体质点运动是无规则的，各点的速度和压力在时间和空间上都具有随机性和不确定性。其次，紊流比层流具有更高的能量耗散。这主要由于流体质点紊动产生的附加剪切效应和涡流的形成，从而导致摩擦阻力和水头损失增加。此外，紊流相比于层流能够更有效地传递动量、热量和质量。一般而言，紊流在雷诺数较高的情况下出现，例如在水利工程中的流动通常呈现为紊流状态。

在流体力学中，雷诺数是一个重要的无量纲参数，用于区分流体的流动状态。通过雷诺数可以判断流动是处于层流还是紊流状态。雷诺数的定义公式为： 

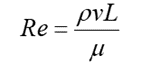   (1)

其中ρ是流体密度（kg/m3），v是流速（m/s），μ是流体的动力粘度（Pa·s 或 N·s/m2），L是特征长度（m）。特征长度在计算雷诺数时至关重要，它用于表征流体流动的情况，其选择取决于具体的流动条件和研究问题。对于固体颗粒在流体中的运动，L一般选择为固体颗粒的直径。如果是液体流动，对于外流问题，L通常取流体前方障碍物的主要尺寸，例如圆柱形桥墩的直径或飞机机翼的弦长。在内流问题中，对于圆形管道流动，L取圆管直径；对于非圆形管道流动，L一般取水力半径。

图1 流体不同流动状态

根据雷诺数的大小，水流流动状态可以分为层流、过渡流和紊流（如图1所示）。当雷诺数较低时，流动呈层流状态。当雷诺数处于层流和紊流之间的过渡区间时，流动状态不稳定，可能表现为层流或紊流，具体取决于外界条件和扰动。当雷诺数较高时，流动呈紊流状态。

在桥渡设计中，层流状态对应于低流速条件下的水流行为，如静水环境或缓慢流动的河流。然而在大多数情况下，水流的流动常表现为紊流形态，如流速较大的溪流或洪水期间的河流。在这些条件下，桥梁基础和结构需要承受较大的水动力作用力，因此在设计时必须考虑抗冲刷措施和结构的加固。

1.4 临界流

当明渠中水流受到干扰微波后，若干扰微波向上游传播的速度为零，这正是急流与缓流这两种流动状态的分界，称为临界流。此时水流的惯性力作用与重力作用恰好相等，弗劳德数为1。

弗劳德数是一个无量纲数，用于描述流体流动中的惯性力和重力之间的比值，其定义公式为：    

(2)

其中v是流速（m/s），g是重力加速度（9.81 m/s2），h是水深（m）。

临界水深是指在明渠流动中，当水流处于临界流状态时的水深。从能量的角度来看，临界水深是指在明渠流动中，流体单位重量液体对经过断面最低点的基准面的总机械能处于最小值时的水深。对于明渠流动的任一过流断面，单位重量液体对经过断面最低点的基准面的总机械能为： 

     (3)

其中h为水深，α为动能修正系数。在流体力学中把机械能E _S 称为断面单位能量或断面比能。

图2 断面比能曲线图

当明渠过水断面的形状、尺寸和流量一定时，断面单位能量E _S 便为水深h的函数（如图2所示）。图中E _S 与h的关系曲线以E _S 轴和45°线为渐近线，且存在极小值。水流在极值处称为临界状态，相应的水深称为临界水深h _c 。

临界水深的计算公式可根据上述定义求出， E _S 与h的关系曲线的极值点C所对应的水深便为临界水深h _c 。对式(3)求导令其等于零，即可确定临界水深。

  (4)

其中dA/dh为过流断面面积随水深h的变化率，它恰等于水面宽度B。则由式(4)可得临界水深的通用计算公式： 

     (5)

当给定渠道流量、断面形状和尺寸时，就可以由上式求得hc值。由上式可知，临界水深h _c 仅与断面形状、尺寸和流量有关，而与渠底坡度及壁面粗糙系数无关。

临界流用于判断水流的状态，在实际应用中，和临界流状态进行对比，主要是来判断下游对上游有没有影响，这也就决定了在对水流进行分析时是否需要考虑下游的影响。在桥渡设计中，临界水深的概念受到了广泛的应用，如桥下水流图式的判别、小桥和涵洞孔径计算、桥面和路基高程设计等。

1.5 缓流和急流

在水力学和河流动力学中，急流和缓流是描述明渠水流状态的重要概念。明渠水流在临界水深时的流速称为临界流速，以v _c 表示。当明渠水流流速小于临界流速时，称为缓流；大于临界流速时，称为急流。

如图3所示，明渠中的急流与缓流在水流现象中有显著差异。缓流中水深较大，流速较小，干扰波既能向上游传播也能向下游传播。相较之下，急流中水深较浅，流速较大，在急流渠道中干扰波只能向下游传播。这是因为在急流中，断面平均流速ν大于静水中的波速 , 因此局部扰动波不能向上游传播；而缓流中流速则相对较小，干扰微波既能顺水流方向朝下游传播，又能逆水流方向朝上游传播，从而引起障碍物前长距离的水流壅高现象。

图3 急流与缓流现象

明渠的水流状态还可用断面单位能量E _S 来判断。当水流为缓流时， v<v _c 。这表明水流处在E _S 与h关系曲线的上支（见图2），此时E _S 随着水深h的增加而增加，即dE _S /dh>0；当水流为急流时，v>v _c ，则h<h _c ，这表明水流处在E _S 与h关系曲线的下支，E _S 随着水深h的增加而减小，即dE _S /d _h <0。

在断面形状、尺寸和流量一定的棱柱形渠道中，顺坡均匀流水深恰巧等于临界水深时的渠底坡度定义为临界坡度，记为i _c 。当渠道实际坡度小于某一流量下的临界坡度时，即i<ic，从而h>h _c ，则渠道中的水流为缓流；当渠道实际坡度大于某一流量下的临界坡度时，即i>i _c ，从而h<h _c ，则渠道中的水流为急流。

除了可用临界流速v _c 、临界水深h _c 、断面单位能量E _S 或者临界坡度i _c 进行判别外，还可用弗劳德数Fr进行判别。当Fr<1时，水流为缓流；Fr>1时，水流为急流。

在桥渡设计中，明确建桥后桥位河段的水流和泥沙运动状态是桥孔计算的基础。然而，实际桥位河段的水流和泥沙运动非常复杂，并且河段水流存在缓流和急流两种水力性质完全不同的状态。考虑到目前绝大多数桥位处于缓流河段，因此在一些假定和实验的基础上，对缓流河段提出了简化水流图式。河段水流图式不仅反映了建桥后水流、泥沙运动和河床的变化，还揭示了桥孔长度、桥前壅水和桥下冲刷三者之间的关系。这些图式可以作为桥孔计算的分析依据，有助于工程师在设计过程中合理规划桥梁结构，确保桥梁的安全和稳定。

2 水力学基本理论

2.1 连续性方程

连续性方程是流体力学中描述流体质量守恒的基本方程，它表明在一个封闭系统内，质量不会凭空产生或消失。流体运动的连续性微分方程可表示为： 

    (6)

其中ρ是流体密度(kg/m ³ )，v是流体速度矢量(m/s)，"??" 表示散度算子。

在恒定流条件下，流体密度不随时间变化，因此?ρ/?t=0，上式可以简化为： 

    (7)

对于恒定不可压缩流体，ρ为常数，则上式可以写成： 

   (8)

图4 恒定流控制体示意图

在恒定总流中取一微小流管为控制体，它的控制面由过水断面1，2以及流管壁面所组成（如图4所示），那么恒定不压缩总流的连续性方程则可通过式(8)对控制体积分求得。设总流控制体的体积为V，其微元体积为dV，则有： 

    (9)

根据高斯定理，可将式(9)的体积分改写成面积分： 

    (10)

其中A为总流控制面面积，u _n 为控制面上各点的流速矢量在外法线方向的投影，曲面积分中 为通过总流控制面的体积通量。由式(9-10)可得：   

     (11)

在总流控制面中，由于侧表面上un=0，于是式(11)可以简化为： 

 (12)

式中，A ₁ 、A ₂ 分别为总流进出口过流断面面积。第一项取负号是因为流速u ₁ 与dA ₁ 的外法线方向相反。令v ₁ 、v ₂ 分别为过水断面1，2的平均流速，应用中值定理则可以得到：    

    (13)

上式即为恒定不可压缩总流的连续性方程。

在桥渡设计中，恒定流连续型方程通常用于确定小桥桥下的天然水深。根据水力学明渠均匀流公式，通常采用试算法确定天然水深。具体步骤如下：首先假定一个天然水深值，然后根据河床断面图计算过水面积A和水力半径R。接着，使用公式(13)和下文中介绍的谢才-曼宁公式计算流量，并与设计流量进行比较。如果计算结果与设计流量的差异不超过5%，则假定的水深可认为是所求的天然水深。否则，需重新假定水深并重复上述计算，直到结果符合要求为止。

2.2 能量方程

恒定流能量方程是流体力学中描述流体流动过程中能量守恒的基本方程。它在水利工程和水力学中起着重要作用，用于分析流体在不同断面之间的能量转换和损失。

对于理想流体，恒定流能量方程通常以伯努利方程的形式表示： 

      (14)

其中  是动能项； 是压能项，p为压力(Pa)；z是位能项(m)。

对于实际流体，则必须考虑能量损失，那么能量方程为： 

     (15)

其中h _w 是能量损失(m)，包括沿程损失和局部损失。

恒定流的能量方程被广泛应用于多个领域，包括皮托管、文丘里流量计以及抽水泵的设计。在桥渡设计中，恒定流能量方程也被应用于小桥涵洞设计中的桥前水深确定。小桥桥下的水流图式与后文中介绍的宽顶堰流相似，按照下游天然水深的大小可分为自由式出流与淹没式出流两种情况。当小桥下游的天然水深h _t ≤1.3h _c 时，桥下水流为自由式出流，此时桥下水深为临界水深h _c 。对桥前水深断面和桥下水深断面建立能量方程： 

  (16)

由于计算点均取自两个过水断面的自由液面处，p _H 和p均等于大气压强，其相对压强等于零。因此，可以依据上式推算出桥前水深H的表达式： 

   (17)

其中v _c 为临界流速(m/s)；v _H 为桥前水深断面的行近流速； 为流速系数，ζ为局部损失系数。

当小桥下游的天然水深h _t ＞1.3h _c 时，桥下的临界水深被下游的天然水深淹没，桥下水流则表现为淹没式出流。采用相同的方法在两个过流断面处建立能量方程： 

   (18)

则桥前水深H为： 

   (19)

其中v为桥下流速(m/s)。

2.3 动量方程

动量方程是动量定理在工程流体力学中的应用，它反映了流体运动的动量变化与作用力之间的关系。动量方程的主要作用是求解力的问题，特别是流体与边界面之间的相互作用力问题。

对于一个固定的控制体，其动量方程可以表示为： 

  (20)

其中 ∑F 为作用在控制体内流体上的合外力，包括体力和面力； 为控制体内流体动量对时间的变化率； 为单位时间内通过全部控制面的动量矢量和，即为单位时间内流出与流入控制体的动量差。

对于常见的恒定不可压缩总流，式(20)可以化简为非常简单的形式。取图4所示总流流束为控制体，则总流控制面中只有A1、A2两过流断面上有动量交换。因此，对于恒定（ ）不可压缩（ρ为常数）总流，式(20)可以简化为： 

(21)

由于流速u在过流断面上的分布通常难以准确确定，在工程实际中一般用断面平均流速v代替u计算总流的动量。然而，考虑到实际流速分布的不均匀性，需要引入动量修正系数β进行修正。β定义为实际动量和按照平均流速v计算的动量的比值。具体表示为： 

   (22)

β值的大小与总流过流断面上的流速分布有关，过流断面上的流速分布越不均匀，β值则越大。在工程计算中一般取β=1。

那么动量方程可以改写为： 

    (23)

考虑恒定不可压缩总流的连续性方程A ₁ v1=A ₂ v ₂ =Q，则上式可以写成： 

    (24)

这便是恒定不可压缩总流的动量方程。

在桥渡设计中，桥墩在水流中会受到冲击力，这个冲击力主要来源自水流动量的变化。动量方程用于计算桥墩处的水流冲击力，助力于设计桥墩的尺寸和形状，确保其能够承受流体动力。此外，水跃是急流转为缓流时产生的能量消散现象，常发生在桥梁下游。动量方程用于分析和预测水跃的位置和高度，从而有助于设计桥梁下游的消能措施，防止水流对下游河道的冲刷。

2.4 谢才-曼宁公式

谢才公式和曼宁公式是水力学中用于计算明渠流动的两种经典公式。它们在桥渡设计、渠道设计以及其他水利工程中均受到了广泛的应用。

谢才公式由法国工程师安东尼·谢才于1775年提出，用于计算明渠流动的平均流速。公式表示为：  

    (25)

其中v是断面平均流速（m/s）；C为谢才系数（m ^1/2 /s），其取决于流体的粘性、流道的粗糙度以及流动状态；R是水力半径（m）；i是渠道的底坡，即水流的水力坡降。

水力半径 R是明渠均匀流计算中的一个重要参数，定义为： 

   (26)

其中A是过水断面面积（m2），P 是湿周（m），即与水接触的渠道周长。

许多学者对谢才系数C值进行了研究，并得到一系列经验公式。其中最为简便而应用广泛的是曼宁公式： 

     (27)

其中n是曼宁糙率系数，反映渠道表面的粗糙程度对水流的影响，通常通过经验值和现场测量确定。对于一般管道和人工渠道， n主要取决于壁面粗糙突起物的大小、形状和分布；对于天然河道，n则与河床沙石粒径和形状，沙波大小、形状和变化，岸滩水草树木的疏密程度，以及河道水位变化等有关。

在桥渡设计中，准确计算桥下流速和流量是确保桥梁稳定性和安全性的关键。谢才-曼宁公式可以用于计算桥下流速，进而确定桥下流量：     

    (28)

3 桥渡设计中的水力现象及原理

3.1 圆柱绕流

流体在固体边界内（如管道、明渠中）的流动，是内流问题；流体绕过物体时的流动，则为外流问题。绕流问题在工程和自然界中广泛存在，如水流经过桥墩、船舶的阻力分析、风对建筑物的作用等。圆柱绕流问题涉及复杂的流体动力学现象，包括边界层分离、涡流生成和流体阻力等。

图5 不同雷诺数下的圆柱绕流现象

圆柱绕流可以根据雷诺数的不同分为几种典型的流动模式（如图5所示）：

（1）低雷诺数流动（Re<1）

在Re<1时，流场中的粘性力相对于惯性力占据主导地位。在极低雷诺数下，流动呈现稳定的层流模式，圆柱上下游的流线前后对称，没有涡流和分离现象。

（2）中等雷诺数流动（1 < Re < 200）

在这一范围内，圆柱上下游的流线逐渐失去对称性。随着雷诺数增加，边界层开始分离，分离后的流体在圆柱下游形成一对固定不动的对称漩涡（附着涡）；当Re > 40时，圆柱后缘上下两侧的漩涡开始周期性地轮流脱落，形成规则排列的涡阵，这种涡阵称为卡门涡街。

（3）高雷诺数流动（Re > 200）

在这种情况下，流体的惯性力占主导地位，流动变得非常不稳定，圆柱后侧的“涡街”逐渐失去规则性和周期性。随着雷诺数的进一步增大，流动变得湍急，层流边界层可能会转变为紊流。

当流体绕经圆柱时，圆柱受到的流体阻力主要包括摩擦阻力和压差阻力，这两者之和被称为绕流阻力。摩擦阻力是指作用在物体表面上的切向力，由于流体的黏滞性所引起。对于非流线型物体，压差阻力则源于边界层分离在物体尾部形成的漩涡。漩涡区的压强较物体前部的压强低，从而在流动方向上产生压强差，形成作用于物体上的阻力。

摩擦阻力和压差阻力均可表示为单位体积来流的动能ρU ² _∞ /2与某一面积的乘积，再乘一个阻力系数的形式，即

   (29)

其中U _∞ 为来流速度；C _f 和C _p 分别代表摩擦阻力系数和压差阻力系数；A _f 为切应力作用的面积，A _p 为物体与流速方向垂直的迎流投影面积。

圆柱受到的绕流阻力可以表示为： 

     (30)

其中C _D 为绕流阻力系数，其主要决定于雷诺数，还与物体表面粗糙度、来流的紊流强度以及绕流物体的形状有关。C _D 值一般由实验确定。

在桥渡设计中，桥墩在河流中的阻力和涡流产生对结构安全性和抗冲刷设计至关重要。由圆柱绕流引起的卡门涡街现象是流体动力学所研究的一种重要现象，出现涡街时流体对物体会产生一个周期性的交变横向作用力，如果力的频率与物体的固有频率相接近，就会引起共振，甚至使物体损坏。通过圆柱绕流理论，可以优化桥墩形状和尺寸，减少阻力和涡流对桥墩的影响。

3.2 宽顶堰流

许多水工建筑物的水流性质，从工程流体力学的观点来看，一般都属于宽顶堰流。例如，小桥桥孔的过水，无压短涵管的过水，水利工程中的节制闸、分洪闸、泄水闸等。

图6 宽顶堰示意图

宽顶堰是指堰体厚度(δ)与堰上水头(H)之比在2.5与10之间的堰，具体分为有坎和无坎两种。有坎宽顶堰流由于堰坎的存在，使得水流在垂直方向受到束缩，导致水面跌落。而无坎宽顶堰流虽无底坎的阻碍作用，但由于受到两边翼墙造成的平面束窄，水面也会发生跌落现象（如图6所示）。流经平底进水闸、桥墩之间、隧洞或者涵洞进口以及由施工围堰束窄河床的水流，均属于无坎宽顶堰流。

宽顶堰上的水流现象是十分复杂的。根据其主要特点，宽顶堰流分为自由式和淹没式两种类型。下面重点讨论自由式无侧收缩宽顶堰流的水力计算，然后再就淹没因素对堰流的影响进行讨论。

图7 自由式宽顶堰流示意图

对于下游水位较低的自由式宽顶堰溢流，其流动特点如图7所示，水流经堰坎进口后，在堰上发生自由水面跌落现象。水面在收缩断面1-1处出现最大跌落，该处水深小于临界水深。此后，堰顶水流保持急流状态，并在出口后产生第二次水面跌落。

以宽顶堰顶端为基准面，对图中的n-n截面以及1-1截面建立能量方程： 

    (31)

其中p ₀ 为标准大气压强。令堰前总水头 ；h ₁ =ψh _c ，其中ψ为垂向收缩系数。则可以根据上式计算出流速公式： 

  (32)

其中流速系数 。令k=h _c /H ₀ ， ，则自由式无侧收缩宽顶堰流量公式为： 

   (33)

其中m为宽顶堰的流量系数，取值范围在0.32~0.385之间。

自由式宽顶堰堰顶上的水深小于临界水深，即堰顶上的水流为急流。从图7可见，当下游水位低于坎高时，下游水流绝对不会影响堰顶上水流的性质。相反，淹没式宽顶堰是指堰顶下游水深对水流产生显著影响，导致堰上游水位和堰顶水位之间的能量关系发生变化。淹没式无侧收缩宽顶堰的流量计算通常采用淹没系数进行修正。

宽顶堰流及公式本质是反映了有限区段内不同稳定状态流动的转变，这种转变主要体现在水面高低的变化。只要流动是连续的，前后两个流动状态是相对稳定的，区段的长度是有限的，沿程水头损失可以忽略不计，都可以作为宽顶堰流进行分析。宽顶堰对堰体厚度与堰上水头之比进行了限定，这种限定的目的就是为了保证堰上的流动是相对稳定的，且可忽略沿程水头损失。若是窄顶堰，其周围的流动更为复杂，不稳定，不能套用宽顶堰的分析方法。当堰顶过宽时，沿程水头损失不可忽略，此时也不能作为宽顶堰流。

在桥渡设计中，流经小桥桥下的水流由于两边翼墙造成的平面束窄作用，进入桥孔时会发生侧向收缩，导致桥孔过水断面面积减小，上游水位抬高。通过小桥桥下的水流图式与宽顶堰类似，因此采用宽顶堰理论作为小桥孔径计算的理论依据。

3.3 水跃与水跌

水跃是明渠水流从急流状态过渡到缓流状态时水面骤然跃起的局部水力现象，如图8所示。水跃伴随明显的水面高度上升和能量损失，是一种常见的非恒定流现象。它可以在溢洪道下、泄水闸下、跌水下形成，也可以在平坡渠道中闸下出流时形成。

图8 水跃现象示意图

在水跃发生的流段内，流速大小及其分布不断变化。水跃区域的上部为从急流冲入缓流流所激起的表面漩流，翻腾滚动，饱掺空气，叫做“表面水滚”。下部是水滚下面的主流区，流速由快变慢，水深由浅变深。通常将表面水滚的始端称为跃首或跃前断面，该处的水深称为跃前水深；表面水滚的末端称为跃尾或跃后断面，该处的水深称为跃后水深。跃前与跃后水深之差称为跃高。跃前跃后两断面的距离称为水跃长度。

水跃前后的水深可以通过动量方程和能量方程进行计算,主要公式如下： 

   (34)

其中h ₁ 是跃前水深，h ₂ 是跃后水深，二者合称为共轭水深。

水跃现象不仅改变了水流的外形，也引起了水流内部结构的剧烈变化，随着这种变化而来的是水跃所引起的大量的能量损失。研究表明，水跃造成的能量损失主要集中在水跃区域，即图8所示的断面1-1、2-2间的水跃段内，仅有少量分布在跃后流段。因此，通常均按能量损失全部消耗在水跃区来进行计算。单位重量水体的能量损失（ΔE）可以表示为： 

   (35)

在水利工程中，水跃现象多被应用于消能设施的设计，如溢洪道和底流消能池，通过水跃消耗多余的动能，保护下游结构。此外，水跃也可用于调节水流状态，确保下游水工结构和河道的稳定。

水跌现象是指明渠水流从缓流状态过渡到急流状态时水面急剧降落的局部水流现象。这一现象多发生在明渠底坡突然变陡或下游渠身断面形状突然扩大的地点。水跌是明渠水流中的一种重要水力现象，其发生不仅与流体的动力特性有关，还受到地形变化的影响。

跌水是连结上下游渠道的防冲建筑物，分为直跌式和陡坡两种类型。直跌式跌水是指水流呈自由坡状态时直接跌入下游段，而陡坡跌水则是水流沿斜坡面流动并与下游连接。跌水多用于落差集中的地方，也常与水闸、溢流堰等建筑物相结合，用作渠道上的退水及泄水设施。根据落差的大小，跌水可以设计成单级或多级。在陡坡涵洞的出水口设计中，通常采用急流槽、消力池、消力槛、人工加糙以及多级跌水等措施对河床进行处理，以实现水流的消能和降速。这样不仅可以有效防止河床被冲刷，还能确保水流的平稳过渡，保障渠道和相关水利设施的安全和稳定。

4 结束语

自然界中天然河道水流，一般情况下属于恒定非均匀水流，发生洪水涨落时属于非恒定非均匀水流，甚至夹带泥沙，属于固-液两相流，水力现象比较复杂。在桥渡设计中，涉及冲刷计算、桥孔计算、调治建筑物布置以及方案比选等都要以水力学计算为工作基础，其中以大于或等于某设计频率的流量选取尤为重要，决定了桥下抗冲流速以及桥前水位雍高两项安全性原则，因此，掌握好水力学基础理论知识对于桥渡设计有着非常大的实际意义。

感谢西南交通大学杨庆华教授的宝贵意见和建议！杨庆华教授对水力现象的直观解释以及对理论原理的感性理解使作者深受启发！