知识点:消声器 我们曾在“消声降噪技术 — 6 阻性消声器的常见类型和应用”对室式消声器(Plenum Chamber Silencer, 暖通空调中也常称之为消声静压箱)的消声性能做过简单介绍。考虑到室式消声器的形式在通风空调系统中使用得比较多,并且很多通风隔声窗系统就是一种特殊形式下的室式消声器,因此,本次我们对室式消声器的消声性能的特征和预测计算方法,做一个较为深入的介绍。 室式或者消声静压箱通常配备在通风空调系统的风机出口与通风管路之间,主要起到两方面的作用:1) 平缓风机出口的湍流,使得出口气流均匀平稳;2) 降低来自风扇的噪声。从声学的角度来说,消声静压箱可以看成有一个进风口和一个出风口的小房间。如果小房间内壁面贴上吸声材料,那消声静压箱就相当于扩张式阻抗复合消声器;如果房间内壁面没有贴上吸声材料,那消声静压箱就是一个单纯的扩张式抗性消声器。
知识点:消声器
我们曾在“消声降噪技术 — 6 阻性消声器的常见类型和应用”对室式消声器(Plenum Chamber Silencer, 暖通空调中也常称之为消声静压箱)的消声性能做过简单介绍。考虑到室式消声器的形式在通风空调系统中使用得比较多,并且很多通风隔声窗系统就是一种特殊形式下的室式消声器,因此,本次我们对室式消声器的消声性能的特征和预测计算方法,做一个较为深入的介绍。
室式或者消声静压箱通常配备在通风空调系统的风机出口与通风管路之间,主要起到两方面的作用:1) 平缓风机出口的湍流,使得出口气流均匀平稳;2) 降低来自风扇的噪声。从声学的角度来说,消声静压箱可以看成有一个进风口和一个出风口的小房间。如果小房间内壁面贴上吸声材料,那消声静压箱就相当于扩张式阻抗复合消声器;如果房间内壁面没有贴上吸声材料,那消声静压箱就是一个单纯的扩张式抗性消声器。
消声静压箱的特征尺寸d通常设计得比声波的波长λ大很多,即满足d >>λ的条件,其中的声场可以看作是类似于房间内的声场,是直达声和混响声的叠加(当然,这一假设在低频不成立)。
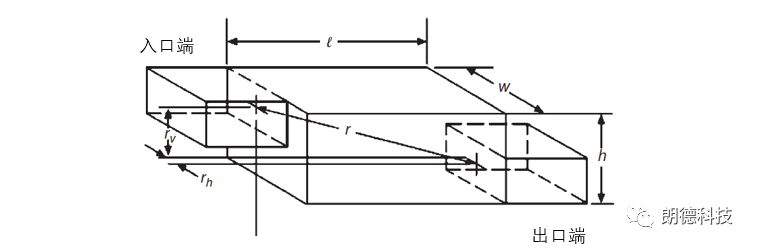
由消声静压箱入口进入箱内的声能,一部分直接辐射到出口段,另一部分经过箱体壁面的一系列反射后进入到出口段,其余的部分被箱体壁面的吸声材料吸收掉。
假设在箱体内的声场是混响声场,并且d >>λ,根据室内声场的原理,直接进入到出口端的声能量将正比于出口的面积,并反比于出口到入口的距离的平方。如果出口和入口不是正对的话,那还需要加上一个指向性因子;如果出口和入口在同一个平面内,那么这一项将消失为零。箱体内混响声能部分到达出口端的部分也是与出口端的面积以及箱体内的混响声能成正比,而混响声能的大小又受箱体壁面的吸声的影响。这个就是Well提出来的分析静压消声箱传声损失的方法。
2.1 Well计算模型
Well[1]在做了以上分析后,给出了内壁具有吸声内衬的消声静压箱的传声损失的计算公式:
式中 α为内衬吸声材料的吸声系数,S为内衬吸声材料的面积, SE为室的进、出口的横截面积,r为进、出口中心之间的距离,Q为指向性因子(Q在Well模型中取2,在Cummings模型中取4),θ为r与l之间的夹角。公式中的第二项也经常写成房间常数R的倒数。cosθ由下式计算。
上面计算传声损失的公式在出口和入口处于同一个平面时,第一项消失,就退化为我们在“消声降噪技术 — 6 阻性消声器的常见类型和应用”给出的计算公式。
Well的计算方法是在假设箱体的尺寸相对于声波波长大很多条件下推导出来了,因此该计算方法只适用于波长远小于静压箱特征尺寸的情况。根据管道内截止频率的公式,方管和圆管的截止频率为:
对于低于截止频率的声波,在管道内只能产生平面波的传播模式,而不能产生高次波的模式,传声损失的计算公式将不再适用。
为了验证计算方法的可靠性,Well对一系列尺寸的静压箱进行了测量,在对比了测量和计算结果后,Well得出结论:对比较小的开口以及在高频范围内,计算得到的传声损失与测量结果接近,对于在接近截止频率以及截止频率以下的频段,测量得到的传声损失要比计算值低5~10dB。事实上,Well的计算公式在1000Hz以及以上频率才较为可靠。
2.2 Cummings计算模型
Cummings[2~3]提出了分别针对低频和高频段的计算模型。在低频模型中,假设在出口段和入口段中的管道中仅有平面波传播,而高次声波模式仅在箱体内被激发;在高频模型中,假设在出口段和入口段中有一系列高次模式的声波被激发。
低频模型:
在低频模型中,入口段管道中的声波看成是入射声波和反射声波的叠加,而在出口段管道中仅考虑入射声波,而没有反射声波(即出口端假设为消声末端)。箱体内的声场被看作是直达声与高次模式声波的叠加,在箱体与进、出口段的交界面,通过声压连续和速度连续条件,来确定各种模态声波的系数。
这个其中的计算过程涉及到一系列公式,在此不一一列出。
高频模型:
在高频模型中,入射声场看作是一系列高次模式声波,Cummings采用射线声学的方法得到和Well的分析方法类似的结果,仅是其中的吸声系数由Well公式中的赛宾吸声系数换成了统计吸声系数。另一个差别是Q在Well模型中取2,而在Cummings模型中取4。
2.3 无吸声内衬的Ih模型
李中国[4]提出了计算无吸声内衬条件下静压箱的模型,他假设箱体内为无源的,并且所有的边界为刚性的,除了进、出口端。他将静压箱看作是活塞激发的刚性壁面的管道,将系统简化为两端网络,给出了传声损失用传递矩阵表示出来的表达式。
2.4 ASHRAE计算模型
在Well模型的基础上,Mouratidis 和 Becker在2014年提出了改进的计算方法,并与他们实验得出的结果更加接近,该计算模型被ASHRAE采纳。
在高于截止频率的高频段,ASHRAE给出的计算方法首先计算进、出口之间没有夹角下的传声损失,再加上夹角修正OAE,并把对数函数改写成指数函数的形式,定义了2个系数b=3.505和 n=-0.359,公式中的其它量与Well模型中的一样。
式中在开口靠近墙中心时Q取2,靠近墙角时Q取4。式中OAE为进、出口之间夹角修正,在截止频率上的频段,按照下表取值(对于角度处于表中角度之间的OAE值,采用线性插值获得):

在截止频率以下的低频段,采用下面的公式计算:
其中的面积系数Af和墙面效应系数We由下表确定:

在截止频率下的频段,OAE按照下表取值(对于角度处于表中角度之间的OAE值,采用线性插值获得):

Li[5]采用了箱体边长为15cm的立方体静压箱,进、出口管道直径为3.5cm(该静压箱对应的截止频率为5760Hz),分别在无声衬和有声衬条件下的实验与计算结果的对比。

在无声衬的条件下,可以看出,在1000Hz以下实测得结果与Ih的模型计算结果还是能较好地吻合,在1000Hz以上的频段,实测结果略高于模型的计算结果。
对于有声衬情况,Cummings的高频模型采用赛宾吸声系数时的计算结果要大于采用统计吸声系数的结果。另外,采用Well模型的计算结果比Cummings之间也存在着微小的差异,这主要是由于指向性因子选择的原因。
对比有无声衬两种情况下的传声损失,可以看出在箱体内采用声衬可以有效改善高频段的传声损失。

下图中给出了采用较大的静压箱的测量与计算结果的对比,箱体的边长为98cm,进、出口管道的直径为9.5cm,对应的截止频率为2122Hz,采用吸声内衬。

相关推荐链接:
