知识点：反时限过电流保护 一、反时限过电流保护简述 同一线路不同地点短路时，由于短路电流不同，保护具有不同的动作时限，在线路靠近电源端短路电流较大，动作时间较短，这种保护称为反时限过流保护。 反时限过流保护的优点是在线路靠近电源处短路时保护动作时限较短；缺点是时限配合较复杂，虽然每条线路靠近电源端短路时动作时限比末端短路时动作时限短，但当线路级数较多时，总的动作时限仍然很长。 二、反时限过电流保护在原理分析
知识点：反时限过电流保护
一、反时限过电流保护简述
同一线路不同地点短路时，由于短路电流不同，保护具有不同的动作时限，在线路靠近电源端短路电流较大，动作时间较短，这种保护称为反时限过流保护。 反时限过流保护的优点是在线路靠近电源处短路时保护动作时限较短；缺点是时限配合较复杂，虽然每条线路靠近电源端短路时动作时限比末端短路时动作时限短，但当线路级数较多时，总的动作时限仍然很长。
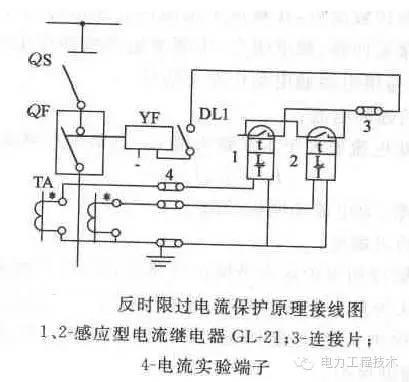
二、反时限过电流保护在原理分析
反时限过电流保护在原理上和很多负载的故障特性相接近，因此保护特性更为优越。
反时限特性曲线的数学模型如下所示：
式中，I——故障电流；
Ip——保护启动电流；
r——常数，取值通常在0－2之间（也有大于2的情况）；
k——常数，其量纲为时间。
动作时间t是输入电流I的函数。
按照IEC标准：
当r<1时，称为一般反时限特性。
其中，上式称为标准反时限特性。
tp为反时限过流保护时间常数整定值。
当r=1时，称为大反时限（甚反时限）特性
其中，上式称为非常反时限特性。
当1
其中，上式称为超反时限特性。当r>2时，称为极端反时限特性
其中，一般反时限特性、非常反时限特性、超反时限特性是目前国际上广泛应用的三种反时限特性。
对于不同的r值，代表不同的应用场合，与不同的被保护设备特性相对应。
例如：
r＝1，常用于被保护线路首末端短路故障电流变化较大的场合。
r＝2，常用于反映过热状况的保护。（电动机、发电机转子、变压器、电缆、架空线等）（因
r>2，虽然较少，但有时也被采用。
如熔丝便是一个具有极端反时限特性的保护（r＝3.5）
对于保护汞整流器的保护其反时限特性要用到r=8。
为发热与电流的平方成正比）
这两种是国内最常用的两种反时限特性曲线。
考虑到实际上被保护设备的故障电流随时都有可能变化，直接应用上述的反时限公式可能得不到正确的结果，可采用如下的电流的积分形式：
热过载（无存储）反时限
忽略了被保护对象故障前的发热。
热过载（有存储）反时限
前三式主要用于线路保护，后二式主要用于诸如电动机等元件的热过载保护。
微机反时限过电流保护的算法实现
对于基本的反时限数学模型：
当r＝1时，微处理器实现相当容易。（只用1个除法运算、1个减法、1个除法）
当r＝2时，微处理器实现也容易。（只用1个除法运算、1个乘法运算、1个减法、1个除法）
2.1直接数据存储法
指预先在微机存储器中存储一张反映时间—电流特性曲线的数据表，然后根据计算出的电流值来查表获得对应的时间。
曲线的斜率如果比较小，存储器内相邻数据间的间隔可以取得比较大；相反，如果斜率比较大，间隔就必须取得较小。间隔的大小和所采用的内差法应该根据不同的拟合对象来决定。
如果要时限对多条曲线的拟合，就需要存储大量的反映不同特性的数据。
特点：
获取动作时间简单且精度高，尤其适合于固有特性曲线和整定值比较少（这样存储的数据量就少）的装置。不适于处理多条曲线，或者为用户提供任意特性曲线的场合。
2.2曲线拟合法
通过一个选配公式来近似拟合特性曲线，典型的是根据最小二乘法原理，利用二次多项式分段拟合特性曲线。
特点：
拟合精度与分段多少、每一段的点数、怎么分段，还和选择的观测点的位置有关。
因此，要获得比较满意的精度，需要做的工作不少。特别是它需要事先知道需拟合的曲线，即知道r值合k值，实现任意r、k对应的曲线有一定的困难。
电气信号的采样分为交流采样和直流采样，交流采样优于直流采样。目前，微机保护装置一般采样交流采样来采样电流信号，得到的是一组等间隔时间的电流信号。
微机中实现开平方运算虽然有C函数库，但是代码长，速度慢，为了避免求取电流有效值时候的开平方运算，两边都取平方：
把上述幂指函数进行改写：
对于任意的正实数R，可以写成R＝M＋N，M为正实数，N为正小数，
因此：
上式有两个部分：前半部分计算实质就是乘、除法，微机计算很容易。 下面的关键就是如何计算后半部分
为分析方便，考虑函数：
无论x（x>0）是什么值，总可以写成如下形式：
对于前半部分，关键是计算（因为n为正整数，n次方实质就是乘法）对于 ，可以采用查表法，事先计算出一条 曲线。因为只有一个变量M，形成的是一条曲线，而不是曲线族，因此存储的数据量少。
再考虑的计算
根据泰勒公式：
因为 ，所以上式为交错级数。
函数 在区间[0,1)之间有极大值 。
所以，截断误差：
由于 的M的范围为那么：
即：
又由于：
那么：
所以截断误差相对值：
这个误差在工程使用上也是偏大的。
从上式也可以看出，如果把a限制在一个小的范围，就可以进一步减小相对误差，提高计算精度。
这时，截断误差相对值
这种精度应该完全可以满足实际的工程要求。
相关推荐链接：
