1、前言

碳纤维复合材料以其比强度高、比模量高，耐高温、耐摩擦、耐腐蚀等优点，在航空航天、汽车、风电、船舶等领域得到了广泛的应用。基于铺层碳纤维复合材料就是将各向异性的碳纤维层材料按照一定的顺序和角度叠在一起，然后通过其它工艺使各铺层紧密的贴合在一起成为一个整体。众多领域复合材料使用量的快速增长催生了碳纤维的分析及优化需求。目前，国内外碳纤维复合材料优化设计的主要设计变量为：几何形状、碳纤维铺层厚度、碳纤维铺层角度和碳纤维铺层顺序，采用多阶段优化设计方法，分别进行几何形状优化、铺层厚度优化与角度优化、铺层顺序优化。这种传统的多阶段优化设计方法要求先优化完一个设计变量再进行下一个设计变量的优化，这不但要求工程师等待一次优化计算完成后提交下一个设计变量的优化计算且忽略了各个设计变量之间的相互影响。本文选用碳纤维增强树脂复合材料，以经典层合板理论为力学计算基础，介绍一种基于HyperStudy优化平台与OptiStruct求解器相结合的综合应用几何形状优化、铺层厚度与角度优化、铺层顺序优化等技术的全新优化方法。

2、模型简述

本文使用的模型如图1所示，该模型长200mm，宽100mm，高100mm，两侧面中心各有一个直径为30mm的圆孔。

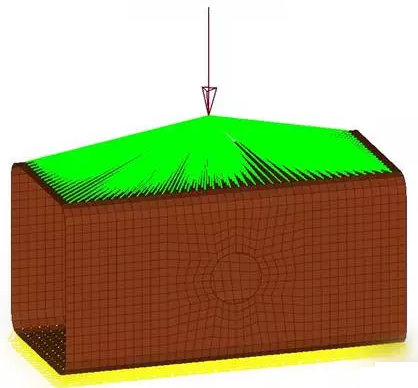
图1有限元模型

模型总共8个铺层，每层厚度均为2mm，铺层角度按0°、-45°、45°和90°依次排列。各铺层具体信息如图2所示。

图2各铺层基本信息

本模型为汽车上某个零件的一部分，本次优化首先要保证结构的刚度（y方向的位移在允许范围内），其次重量要轻。由于原材料和工艺的要求，碳纤维铺层的厚度只能为0.05mm、0.1mm、0.15mm、0.2mm和0.25mm，碳纤维铺层的角度只能为0°、±45°和90°四种角度。另外由于布线的要求，需要在两个侧面开一个直径为30mm的圆孔，但圆孔可以上下移动。

3、优化设计

优化设计三要素为设计变量、约束条件、目标函数。优化设计通常可以归纳为：在一定的约束条件下，选取设计变量，使目标函数达到最小（或最大），其数学表达式一般为：

〖min〗〖f(x)〗x∈X

s.t.g_u(x)≤0u=1，2，m

h_v(x)=0v=1，2，p

式中：x——设计变量，x=[x_1，x_2，，x_n]^T；X——符合一定条件的设计变量的集合，即设计空间；m、p——分别表示不等式和等式约束的个数。

（1）设计变量

本模型以侧面圆孔向上移动的距离和每个铺层的厚度和角度为设计变量，即同时实现了几何形状优化、铺层厚度与角度优化、铺层顺序优化。每个铺层厚度和铺层角度均为离散变量，根据设计的要求设计变量的表达式如下：

X={shape，th1，th2，th3，th4，th5，th6，th7，th8，ori1，ori2，ori3，ori4，ori5，ori6，ori7，ori8}

shape∈[-10，10]

th1，th2，th3，th4，th5，th6，th7，th8∈{0.05，0.1，0.15，0.2，0.25}

ori1，ori2，ori3，ori4，ori5，ori6，ori7，ori8∈{0°，-45°，45°，90°}

式中shape为模型侧面圆孔向上移动的距离，负值表示向下移动.thn为第n层的厚度，orin为第n层的角度。

这17个设计变量在HyperStudy中的设置如图3所示。

图3设计变量

（2）约束条件

本案例约束条件为材料不发生破坏和顶面下降（-y方向）位移小于0.05mm。

目前国内外常用的单层板失效准则有最大应力准则、最大应变准则、Tsai-Hill强度准则、Hoffman准则和Tsai-Wu张量多项式准则。其中Tsai-Wu张量多项式准则是对复合材料的破坏描述最全面的准则，对于2D平面应力状态(σ_3=0，τ_13=0，τ_23=0)，Tsai-Wu张量多项式准则的表达式如下：

F_1σ_1+F_2σ_2+2F_12σ_1σ_2+F_11σ_1^2+F_22σ_2^2+F_6τ_12+F_66τ_12^2=1

其中F_ij+F_i为材料的强度参数，σ_i为正应力，τ_ij为切应力

当F_1σ_1+F_2σ_2+2F_12σ_1σ_2+F_11σ_1^2+F_22σ_2^2+F_6τ_12+F_66τ_12^2≤1时复合材料在弹性变形阶段，材料没有破坏。

约束条件的表达式如下

tsai_wu≤1

disp≥-0.05

式中：tsai_wu=F_1σ_1+F_2σ_2+2F_12σ_1σ_2+F_11σ_1^2+F_22σ_2^2+F_6τ_12+F_66τ_12^2

disp为顶面中心节点的y方向位移。

约束条件在HyperStudy中的设置如图4所示。

图4约束条件

（3）目标函数

本案例是为了在保证结构刚度的基础上实现减重，由于材料密度一样，采用最小体积可等效最小质量。

其表达式如下：

minvolume

式中volume=75025.69×（th1+th2+th3+th4+th5+th6+th7+th8），75025.69为壳单元总面积，volume为模型体积。

目标函数在HyperStudy中的设置如图5所示。

图5目标

......