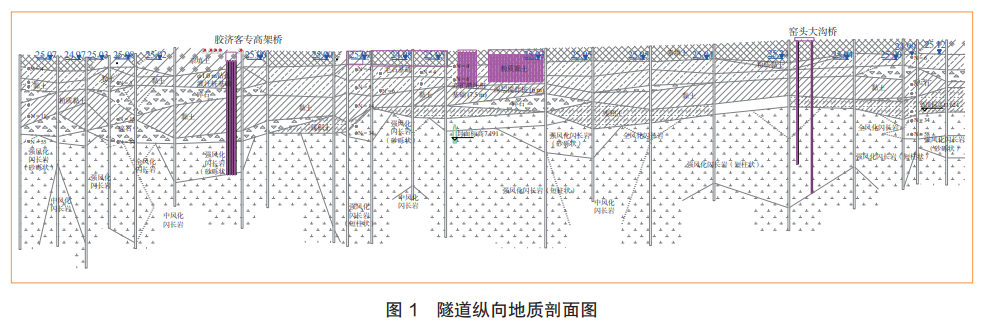
01

   工程概况    

济南地铁 R2 左线历山北路站—二环东路站区间工程，起终点里程分别为CK18+607.365和CK20+691.302，全长2083.937m，区间内采用土压平衡盾构施工。盾构隧道为标准单洞单线圆形断面，线间距为12～25.4m，左、右线覆土厚度为10.5～24.1m。地铁区间隧道主要穿越强风化闪长岩和全风化闪长岩，同时局部地区穿越黏土、残积土和中风化闪长岩等地层。通过查阅隧道纵向地质剖面图，如图 1 所示，并结合施工现场的地质调查，确认该区域并未发现采空区、地表沉降等不良地质现象，也排除泥石流和崩塌等自然灾害的风险。此外，经过钻孔调查，确认在建场地也不存在溶洞、软弱夹层或破碎带等不良地质作用，整体地质条件良好，非常适合采用盾构法进行掘进施工。          

         

02

   盾构掘进参数相关性分析    

地铁区间盾构隧道工程面临复杂多变的地层条件，同一隧道断面往往涵盖多种不同的地层，给数据分析和挖掘带来极大的挑战。因此，传统的环平均值统计方法在此并不适用。为更深入地研究盾构掘进参数的变化特征，本文选取 3 种具有代表性的地层进行分析和挖掘。          

（1）地层一。上部残积土、下部为短柱状强风化闪长岩的复合地层（176 ～ 180 环）。          

（2）地层二。砂砾状强风化闪长岩地层（462 ～464 环）。          

（3）地层三。上部为碎石、下部为全风化闪长岩的复合地层（712 ～ 718 环）。          

在 3 种不同地层条件下，重点研究盾构掘进参数的变化规律，包括刀盘功率、刀盘扭矩、推进压力、总推进力以及推进速度等。          

2.1 盾构掘进参数变化规律          

通过对盾构施工时间的分析，得到盾构掘进过程中各项参数的变化特征，包括刀盘功率、刀盘扭矩、推进压力、总推进力和推进速度等。进一步对比分析不同地层中盾构掘进参数的变化情况。盾构刀盘功率与刀盘扭矩随掘进时间的变化曲线如图 2、图 3 所示。由于刀盘功率是刀盘扭矩与刀盘转速的乘积，而刀盘转速的数值相对较小，对刀盘功率的影响也较小，因此刀盘扭矩是影响刀盘功率的主要因素。可以看出，刀盘功率和刀盘扭矩的变化规律基本一致，由此可知 3 种地层中刀盘功率的差异主要源自刀盘扭矩的不同。          

         

盾构推进压力与总推进力随时间的变化曲线如图 4  和图  5  所示。可以明显看出，推进压力与总推进力的变化趋势大致相同，二者之间具有较强的相关性。盾构机的推进压力主要由油缸产生，用于推动刀盘破岩。当掌子面的岩体强度较大时，需要更大的推进压力，同时总推进力也会相应增加。在对比  3  种地层时，发现推进压力的差距并不显著，其均值分别为 254.789×102kPa 、 282.099×102kPa  和  239.089×102kPa （推进压力的原始数据单位为 Bar ， 1Bar = 100kPa ，为保证数据的原真性，时序图采用原始数据）。其中，地层二的推进压力最大，与总推进力情况类似。原因为砂砾状强风化闪长岩的整体硬度大于碎石与全风化闪长岩的复合地层以及残积土与短柱状强风化闪长岩的复合地层。此外，单一硬岩地层的整体强度大于复合地层，因此在掘进过程中，单一硬岩地层更难破岩和推进。

         

盾构推进速度随时间变化的曲线如图 6 所示。可以看出，地层一的盾构推进速度均值最高，达到 45.463mm/min ，地层三次之，为 37.9953mm/min ，地层二最小，且远远小于地层一和地层三，仅为 7.146mm/min 。这种差异情况与总推进力的表现相吻合，主要是由于地质条件的不同所致。地层二的整体性好、强度高，因此推进困难，导致推进速度较慢。相比之下，地层一和地层三为复合地层，整体性差、岩石强度低，因此容易推进，推进速度更快。

2.2 掘进参数相关性分析          

为深入探究盾构掘进过程中各参数之间的相互影响关系，需要进行参数间的相关性分析。通过相关性分析方法进行判断，利用相关系数 r 量化各掘进参数之间的相互作用程度。相关系数 r 范围为[-1，1]，其正负值表示各掘进参数之间是正相关还是负相关。在进行相关性分析时，主要采用以下3种常用的相关系数。          

（1）皮尔森相关系数：          

          

式（1）中， Cov  为协方差函数； Var  为方差函数。          

（2）斯皮尔曼相关系数：          

          

（3）肯德尔相关系数：          

          

在 3 种相关性分析方法中，肯德尔相关系数适用于分类变量的数据相关性分析。皮尔森相关系数虽然统计效率较高，但其应用条件较为严苛，要求数据必须连续、呈正态分布，并且满足线性关系。而斯皮尔曼相关系数则相对更为灵活，对数据的要求较为宽松，无需满足特定条件，因此适应性更广。鉴于盾构掘进参数中的某些参数（如刀盘转速）并不完全符合正态分布的要求，因而选择斯皮尔曼相关系数进行相关性分析。          

一般情况下，当 |r| ≥ 0.8 时，为极强相关；0.6 ≤ |r| < ? 0.8 时，为强相关；0.4 ≤ |r| < ? 0.6 时，为中等程度相关；0.2 ≤ |r| < ? 0.4 时，为弱相关；|r| < ? 0.2 时，为极弱相关或不相关。          

通过对总推进力、刀盘扭矩、刀盘功率、推进速度、推进压力以及刀盘转速这 6 个盾构掘进参数进行斯皮尔曼相关性系数的分析，得到各地层盾构掘进参数之间的相关性，如表1～表3所示。          

可以发现 3 种地层中，刀盘扭矩与刀盘功率的相关性均达到极强的程度。这一点在图 2 与图 3 的时序图中也得到验证，两者的走势几乎完全一致。此外，刀盘扭矩与推进速度和推进压力的相关性处于中等水平，而与刀盘转速的相关性则较弱。然而，值得注意的是，在地层一中，刀盘扭矩与推进压力的相关系数相对较低。通过观察时序图，推测可能由于前半段的推进压力较为平稳，几乎没有波动，而刀盘扭矩则出现较大的波动。          

在 3 种地层中，刀盘功率与推进压力和推进速度的相关性介于弱相关和中等程度相关之间。而推进速度、推进压力和刀盘转速等其他掘进参数之间也存在一定程度的弱相关，但整体相关性较低。综合以上分析，盾构总推进力和刀盘扭矩与其他掘进参数的相关性较强，因此在后续的盾构掘进参数预测分析中，需重点关注这2个参数。

03

   盾构推力与刀盘扭矩预测    

盾构掘进过程中产生的数据量庞大且维度复杂，人工分析不仅计算繁琐，且容易忽略特征之间的规律。故采用机器学习算法进行数据挖掘，以便更准确地预测盾构参数。由相关性分析可知，总推进力与刀盘扭矩与其他掘进参数之间存在较强的相关性，并且对地质变化更为敏感。因此选取盾构总推进力与刀盘扭矩作为预测对象，并运用支持向量机（SVR）算法，分别预测不同地层的总推进力和刀盘扭矩。          

3.1 SVR预测模型评估指标          

模型评估指标常用  R ²  拟合优度和平均绝对百分比误差（MAPE）作为评估指标，计算公式如下：          

          

在盾构掘进参数预测时，式（4）中的分子表示参数实测值与预测值间的误差，分母表示实测值的离散程度。 R ²  越大，拟合效果越好，当  R ²  的值大于 0.4 时，就可以认为模型的拟合效果良好。MAPE 表示预测值和真实值的误差，其值越小，则误差越小，模型的预测性能也就越好。当 MAPE 的值大于 1 时，代表预测模型的性能较差，需要进一步改进和优化。          

3.2 模型预测结果及分析          

为建立预测模型，对预处理并标准化后的盾构掘进参数进行划分。将每种地层的盾构掘进参数随机分成 10 份，其中 8 份作为训练集，2 份作为测试集。在预测总推进力时，以刀盘扭矩、推进速度、刀盘功率、推进压力和刀盘转速作为输入参数，总推进力作为输出参数，利用这些参数对总推进力进行预测。预测效果的评估采用  R ²  作为评价指标，结果如表 4 所示。而在预测刀盘扭矩时，由于刀盘功率与刀盘扭矩之间的相关性极高，为避免刀盘功率对预测结果的影响，在预测刀盘扭矩时剔除刀盘功率这一参数。同样地，使用之前分好的训练集和测试集，以推进速度、推进压力、刀盘转速和总推进力作为输入参数，刀盘扭矩作为输出参数，对刀盘扭矩进行预测。预测效果的评估依然用  R ²  作为评估指标，结果如表 5 所示。          

由表 4 和表 5 可以看出，当数据集选择“rbf”核函数时，预测效果最佳， R ²  也最高，这表明数据呈现偏线性分布的特征。在对比 3 种地层时，发现 SVR 模型在地层三中的表现最好，而在地层一中的表现相对较差。特别值得注意的是，地层三中总推进力与推进压力的相关性较强，而地层一中则为中等程度相关，这进一步验证推进压力对总推进力预测的重要影响。          

对于刀盘扭矩的预测，地层二的表现最佳，而地层三的表现最差。这与相关性分析的结果并不完全一致，因为地层三中刀盘扭矩与其他参数的相关性最高。结合工程地质分析，发现地层二刀盘扭矩波动剧烈，方差大，离散程度高。根据  R ²  的计算公式，真实值的离散程度会影响分母的大小，离散度越高，分母越大，从而可能导致  R ²  值增大。因此，在比较不同地层的预测效果时，不能仅依赖  R ²  这一个评价指标。然而，在同一地层中比较不同模型的效果时， R ²  评价效果更直观和高效。          

3.3 SVR预测模型优化          

粒子群优化（POS）算法的思想灵感来源于自然界中鸟类捕食的行为，它在多维空间寻优方面有很强的能力，通过随机生成粒子群来代表极值优化问题中潜在的最优解。每个粒子都具有速度、位置和适应值这 3 个特征，其中适应值是通过适应度函数计算得出的，用于评估粒子的优劣。为提升盾构掘进参数总推力和刀盘扭矩的预测精度，采用粒子群优化算法对 SVR 预测模型进行优化。经过优化，各地层中 SVR 模型对盾构总推力和刀盘扭矩的预测结果如表 6 和表 7 所示。          

         

从表             6             和表             7             可以看出，经过粒子群优化算法优化后的             SVR             模型，其预测效果有了显著的提升。不仅             R            ²            值有了明显的提高，而且预测误差也大幅度减少。特别是在地层一中，虽然总推进力和刀盘扭矩的预测结果相对较差，但通过             MAPE             指标的分析，发现地层一的拟合优度确实较低，且误差较高。          

         

以地层一为例，绘制盾构总推进力与刀盘扭矩真实值与预测值拟合曲线，如图 7 和图 8 所示。          

         

           图中横纵坐标分别对应着真实值与误差值。图中的直线为             y             =             x            ，散点到直线的距离为误差值，距离越近意味着误差越小。其中，红色点代表误差在             1%             ～             2%             之间的数据点，绿色则代表误差超过             2%             的点，而淡蓝色的点表示误差在             1%             以内的数据点。由图表结果可知，经过             PSO             优化后的总推进力的预测精度             R            ²                         提升约             3%            ，刀盘扭矩的             R            ²                         提升约             10%            。提升幅度相当显著，充分展示了             PSO             优化算法在提升             SVR             模型预测效果方面的有效性。