高强钢因其可降低结构用钢量和资源消耗,在越来越多的工程中得到了应用,但有关高强钢构件稳定性的研究还比较缺乏,而残余应力又是影响构件稳定性的重要因素。BS700 高强钢(名义屈服强度为 700MPa)由于没有型钢,采用先把钢板冷弯成槽形截面构件,然后对焊形成箱形截面构件,而焊接会使构件截面产生残余应力,目前还比较缺乏有关焊接残余应力对 BS700 槽形对焊箱形截面构件稳定性影响方面的研究,为此对这一问题借助试验和数值分析的方法展开了研究,以期了解残余应力对 BS700 槽形对焊箱形截面构件稳定性的影响。

通过材料拉伸试验,得到了 BS700 高强钢材料的力学性能参数。借助拉伸试验得到了构件开孔时的应力释放系数,运用盲孔法对 BS700 槽形对焊箱形截面构件中部截面的残余应力进行了测试,得到了其截面上相关点位的残余应力值,结合已有研究成果,提出了 BS700 槽形对焊箱形截面构件残余应力分布模式;借助有限元分析软件ANSYS 利用其 APDL 可编程语言编写了可引入几何缺陷和残余应力的非线性屈曲分析模型,利用该模型对长细比分别为 15、20、30、50、70、90,截面宽厚比分别为 10、15、20、25、30、35、40、50 共计 48 个构件区分有、无残余应力进行了非线性屈曲分析,研究了不同宽厚比和不同长细比条件下残余应力对 BS700 槽形对焊箱形截面构件稳定性的影响。

通过研究发现在焊缝处及弯角处存在残余拉应力,其余各处为残余压应力。焊缝处最大残余拉应力水平约为屈服强度的 0.76,腹板中部位置的最大残余压应力值约为屈服强度的 0.14。在已有研究的基础上提出了多折线型的残余应力分布模式,与试验结果对比吻合较好;残余应力对不同宽厚比条件下的构件稳定系数均有影响,总体趋势是随着宽厚比的增加,残余应力的影响逐渐减小,主要原因是在大宽厚比条件下构件呈现局部板件弹性屈曲的现象;残余应力对不同长细比条件下的构件稳定系数均有影响,但在长细比较小或较大时影响相对较小。在长细比位于 20 ~ 70 之间时,残余应力对构件稳定系数的影响较大,通过对比发生板件局部屈曲时的临界长细比发现,二者有重合之处,说明按照常用的等稳性设计时,这些中等长细比范围内的构件对残余应力相对比较敏感,因此,在构件稳定性设计过程中,需注意这一影响因素。

高强钢比普通结构钢具有更高的强度,能节省结构材料使用,但其材料延性差没有明显屈服平台、焊接困难,因此高强钢结构受力性能研究是工程界亟需解决的问题之一。目前高强钢没有型钢仅有板材,需要通过焊接形成各种截面,而焊接产生的残余应力会对构件稳定性产生影响。许多的研究者对高强钢焊接残余应力开展了研究, Rasmussen等对 4 个 690 MPa 高强钢材焊接箱形截面构件的残余应力进行了测量,给出了各板件中残余压应力的范围,并用于后续轴压构件整体稳定性能的计算分析。Beg 等对 690 MPa 的剪切边工字形截面构件开展了残余应力测量试验,提出了 690 MPa 强度的工字形截面残余应力分布模式。Iwatsubo对460 MPa 强度等级 SM570 钢材的焊接箱形截面构件的残余应力进行了测量试验,指出随着板件宽厚比的增大,残余压应力的绝对值总体呈减小趋势。Dae-Kyung 等对由屈服强度 800 MPa 钢材HSA800 制成的短柱残余应力进行了研究。班慧勇等对高强度钢材焊接残余应力分布及轴心受压构件的受力性能方面进行了一系列理论和试验研究,得出了焊接工字形、箱形的截面残余应力分布规律及其对受压构件稳定性的影响。李国强等进行了 Q690 高强钢焊接箱形截面试件残余应力试验,得到了箱形截面的残余应力分布模型。同时,建立数值模型对箱形轴压构件进行了参数分析,基于试验和参数分析结果,给出了焊接箱形截面轴压构件设计的相关建议。舒赣平等对 Q550 高强钢焊接箱形截面构件进行了轴压试验,提出一种焊接箱形截面残余应力分布模型,试验结果初步揭示了轴压构件局部稳定和相关稳定的性能。

BS700 高强钢(名义屈服强度 700 MPa)槽形对焊箱形截面构件已应用于一些桥梁结构中。由于该高强钢没有型钢,采用先将钢板冷弯成槽形截面,然后对焊形成箱形截面与普通意义上的四块板焊接形成的箱形截面不同,涉及这种特殊高强钢截面形式的残余应力研究还很少,本文研究了残余应力对BS700 高强钢槽形对焊箱形截面构件稳定性的影响,为更好的应用该材料奠定基础。

1.1 材料性能试验

为了开展试件的残余应力测试及数值分析计算,对来源于同一批制作试件材料的钢板进行了材料拉伸试验,一共制作了 3 个拉伸试件,其拉伸试验如图 1 所示。

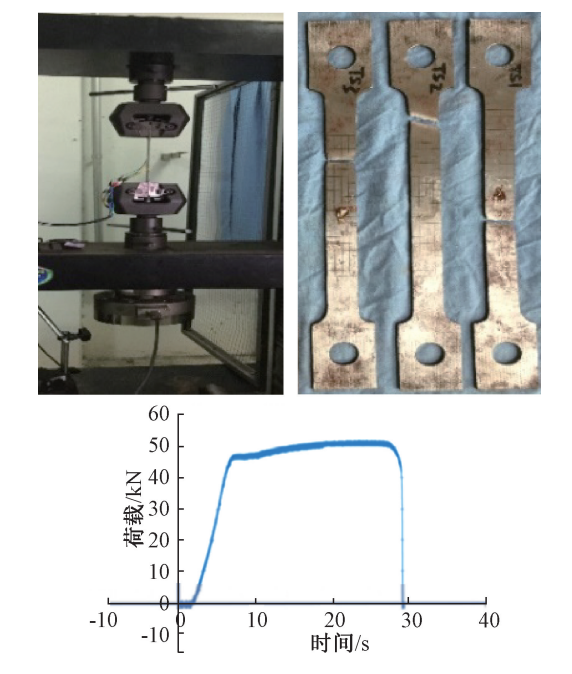
图 1 材料拉伸试验

由于试件属于高强钢,试件破坏时无明显颈缩现象,材料曲线屈服平台比较短,因此采用残余应变为 0.2%时的强度作为名义屈服强度,三个试件的名义屈服强度平均值为 741.6 MPa。

1.2 应力释放系数标定

目前残余应力的测试方法有很多如切条法、X射线法、盲孔法等。本文采用盲孔法测量 BS700槽形对焊箱形截面构件的残余应力。

盲孔法测试残余应力基本原理是在构件表面进行钻孔,破坏原有平衡状态,从而释放应力,应力释放产生应变,粘贴的应变花可以测量出此应变,根据应变花测量的三个应变采用式(1)就可以计算出残余应力。

式中: ε₁ 、ε₂ 和 ε₃ 分别为钻孔后 0°、45°、90°三个方向释放的应变; σ₁ 、σ₂ 为最大和最小主应力; θ 为 σ₁与 ε₁ 的夹角; E 为材料弹性模量; A、B 为释放系数,需要测试前进行标定。标定试验参 照 GB/T31310—2014《金属材料残余应力测定钻孔应变法》中附录 A 的方法。标定试件与待测试件为同一批次材料钢板制成。标定试件先不打孔进行拉伸,打孔后再进行拉伸,试验过程如图 2 所示。 

图 2 标定系数 A、B 照片

系数 A、B 的测量次数最低不少于 2 次,若 2 次比较误差超过 10%,则重新标定。2 次标定得到 A、B 后取其平均值,其计算公式如下:

将测得应变代入(2),得出释放系数 A、B 分别为:A = -0.1223, B = -0.2045。

1.3 残余应力测试

为得到截面残余应力分布规律,对两个试件进行残余应力测试。宽厚比分别为 20、30, 厚度为3 mm,试件的长度 L 不小于截面宽度的 3 倍,在测量点位处两端各预留 1.5 倍试件宽度的长度,以减小端部效应和焊接过程中不均匀热输入产生的不利影响。以 RS2 试件为例说明测定位置情况,测点 1在焊缝上,测点 2 是测点 1 对应的焊缝热影响区距焊缝 20 mm,测点 3 在弯角处距离边缘 5 mm,测定 4在弯角处,距边缘均为 5 mm;测点 5 为无焊缝面板中间位置(距离弯角 30 mm),试件 RS1 的测点位置与试件 RS2 相同,具体测点位置及现场测量如图 3所示。

图 3 测点位置及残余应力测量

1.4 测试结果及分析

根据测量结果并通过计算得到的各试件测点数值如表 1 所示。

表 1 各试件测点残余应力值     MPa

由表 1 可知,焊缝附近的残余拉应力峰值最高,弯角处的残余拉应力峰值大小近乎相等,且均远低于材料的屈服强度,残余拉应力峰值平均值为563.6 MPa,约为钢材实测屈服强度的 0.76,最大峰值应力为 596.2 MPa。弯角处的残余拉应力约为屈服强度的 0.11,残余压应力平均值约为屈服强度的0.14 倍。

结合试验数据和文献资料提出如图 4 所示的残余应力分布模式(因截面左右对称,残余应力分布也假定左右对称,仅画出右半边残余应力分图)。

图 4 残余应力模式

图中 σ_ft 表示翼缘焊缝位置处的残余拉应力,σ_fc 表示翼缘的残余压应力, σ_fwt 表示冷弯角处的残余拉应力, σ_wc 表示腹板的残余压应力; a₁ 、b₁ 、c、a₂ 、b₂ 、d₁ 、e₁ 、g、e₂ 、d₂ 表示残余应力各分布区的长度。其中: σ_ft= (0.7 ~ 0.85) f_y, σ_fwt= (0.05 ~ 0.15) f_y ,σ_fc= -(0.1 ~ 0.25) f_y , σ_wc= -(0.1 ~ 0.2) f_y ,a₁= t ~ 2t, b₁= 0.05b, d₁= t ~ 2t; 其余尺寸可根据应力平衡条件式(3)求得。

式中: σ_r 表示残余应力; b 为截面宽度; h 为截面高度; t 为截面厚度。

为了验证提出的残余应力模式,将 RS2 试件试验数据与提出的残余应力分布模式进行对比,结果如图 5 所示。从图 5 可以看出,提出的残余应力分布模式与试验结果吻合较好。

图 5 残余应力模式与实测数据

利用有限元软件 ANSYS 先建立基本的有限元模型,单元类型采用 Shell 181,该单元可引入几何初始缺陷和残余应力,模型没有考虑截面的冷弯效应,没有倒角。为了确保荷载轴心加载到构件上,在杆件的两端加上了 2 块刚性板 (此板的弹性模量较大)。施加约束时,采用简支约束,约束两端板中央处的节点。其次,建立基本有限元模型后,采用一致缺陷模态法引入局部几何缺陷,残余应力通过编制初应力文件的方式引入基本分析模型模块。读入残余应力后,截面上的轴向应力云图如图 6 所示。

图 6 施加残余应力后截面应力云图

整个有限元计算程序包含基本分析模型模块、几何缺陷引入模块、残余应力引入模块、求解模块和后处理模块等 5 个模块。所有的程序模块都采用参数化语言,方便根据具体数值分析要求更改模型。从材料试验曲线可以看出,该材料具有一定的屈服平台,屈服以后的强化阶段曲线比较平缓,为此材料模型选用理想弹塑性模型。弹性模量为 2.06 × 10⁵MPa,屈服点 0.003398 ,700 MPa。分别对有残余应力、无残余应力情况下的构件进行非线性有限元屈曲分析。

2.1 不同宽厚比条件下残余应力对构件稳定性的影响

截面宽厚比分别设置为 15、20、30、50、70、90,计算了不同长细比下有无残余应力时的 BS700 高强钢槽形对焊箱形截面轴压构件的稳定系数( P_u/P_y , P_u 为极限承载力、P_y 为全截面屈服时承载力),得到的有、无残余应力时的构件稳定系数对比结果如图 7 所示。

a—长细比为 15; b—长细比为 20; c—长细比为 30; d—长细比为 50; e—长细比为 70; f—长细比为 90。

图 7 不同宽厚比下残余应力对稳定系数的影响对比

由图 7 可知,残余应力对宽厚比箱形截面的稳定系数有影响,总体趋势是随着宽厚比的增加,残余应力的影响逐渐减小,主要原因是在大宽厚比条件下构件呈现局部板件弹性屈曲的现象。

2.2 不同长细比条件下残余应力对构件稳定性的影响

将长细比分别设置为 15、20、30、50、70、90,计算了不同截面宽厚比下有无焊接残余应力时的BS700 高强钢槽形对焊箱形截面轴压构件的稳定系数,对比结果如图 8 所示。

a—b/t = 10; b—b/t = 20; c—b/t = 30; d—b/t = 40; e—b/t = 50; f—有无残余应力

图 8 不同长细比条件下残余应力对稳定系数的影响对比

从图 8 可以看出,当构件长细比位于 20 ~ 70 之间时,残余应力对构件稳定系数的影响较大;20 ~ 70区间外,残余应力对构件稳定系数的影响相对较小。从图 8f 可以看出在宽厚比小于 30 时,不同长细比下有无残余应力对构件稳定系数影响较大,最大值超过 10%。同时随着长细比的不同影响也不相同,随着长细比增大,差别越来越大,在某一长细比差别达到最大值,随后差别减小。而产生最大差别时的长细比通常是按照等稳性设计时的最佳长细比,等稳性设计为板件的局部稳定与构件的整体弹性稳定相等。板件的局部应力为:

式中: k 为板两端的约束嵌固系数。

构件的整体稳定系数为:

当两者相等,即 σ = σ_cr 时可得:

式中,难以确定的是约束嵌固系数。对腹板,由于有初始缺陷存在,因此一侧腹板受拉,一侧受压。实际情况下,受压一侧的腹板受到上下翼缘的约束嵌固,其嵌固系数 k 介于一端固定一端自由(嵌固系数为1.28)和两端简支之间(嵌固系数为 4)。当取中间值 2.64 代入式(6)中可得到不同宽厚比条件下的按等稳性设计时长细比,如表 2 所示。

表 2 等稳性设计时长细比

从图 8 可以看出,在长细比为 30 ~ 60、宽厚比小于 30 时,残余应力影响达到最大值,与表 2 计算的长细比数值比较吻合,说明等稳性设计时,对于中等长度长细比构件来说,其稳定性对残余应力相对比较敏感。