钢结构中存在着残余应力，严重影响构件或节点刚度及极限承载力。利用有限元实体模型，通过预定义场功能引入煨弯钢管工艺中产生的热弯残余应力分布。考虑拱脚支承形式、荷载形式、长细比3个因素，研究了热弯残余应力对圆钢管拱结构平面内极限承载力的影响。通过分析得出：不同支承形式和荷载形式下热弯残余应力对钢拱平面内极限承载力的影响在3%以内，当均布荷载作用时热弯残余应力会使钢拱提前进入弹塑性阶段；当正则化长细比在1.30~1.70之间时，热弯残余应力对钢拱平面内极限承载力的影响最为明显，可降低9%。

关键词：钢结构；圆钢管拱；热弯残余应力；平面内稳定；极限承载力

圆钢管拱结构作为一种造型优美、受力合理的结构形式，广泛应用在体育馆、航站楼、火车站等大跨度建筑结构中。近年来，国内外学者对拱结构的极限承载力、平面内外弹性和弹塑性屈曲等问题进行了研究，积累了大量的研究成果。PI等^[1-2]讨论了弹性支承浅圆拱的平面内弹塑性稳定问题。李佳欣等^[3]对工字形截面钢拱进行了弹塑性大变形分析研究。陈玉骥等^[4]分析了剪力滞效应和几何非线性对薄壁拱结构稳定性的影响。

由于钢结构中存在残余应力，会导致钢材提前达到塑性，严重影响构件或节点刚度及极限承载力。针对残余应力对钢拱稳定承载力的影响研究，陈爱国等^[5]对影响两铰抛物线拱弹塑性承载力的因素进行分析，发现残余应力会使钢拱稳定承载力降低3%。GUO等^[6]、郭彦林等^[7]、林冰等^[8-10]基于大量的钢拱极限承载力数值分析结果，得到当正则化长细比在0.25~1.25时，残余应力对钢拱极限承载力影响最大的结论。

以上残余应力对钢拱极限承载力的影响研究中，残余应力的引入模型均采用直构件的圆截面残余应力模型，未涉及热弯残余应力对圆钢管拱结构极限承载力的影响。实际上，在热弯构件残余应力分布方面已取得一定的研究成果，CEGLIAS等^[11]通过X射线衍射法和钻孔法测量了热弯后API5LX70钢管的残余应力。COLLIE等^[12]通过有限元模型实现了圆钢管热弯的应力预测。KIM等^[13]基于试验和有限元分析的结果，得到随着壁厚增加，圆钢管内壁残余应力先增大后减小的结论。HAN等^[14]通过试验测量了圆钢管在热弯过程中产生的纵向残余应力，并基于试验数据提出了圆钢管热弯残余应力模型。

1 计算模型

本文所研究的圆钢管截面外径D为159mm，管壁厚度t为8mm，D/t=19.88，截面面积A为3,795mm²。拱轴线为圆弧曲线，矢跨比f/L取0.10，曲率半径R为3,900mm，如图1所示。

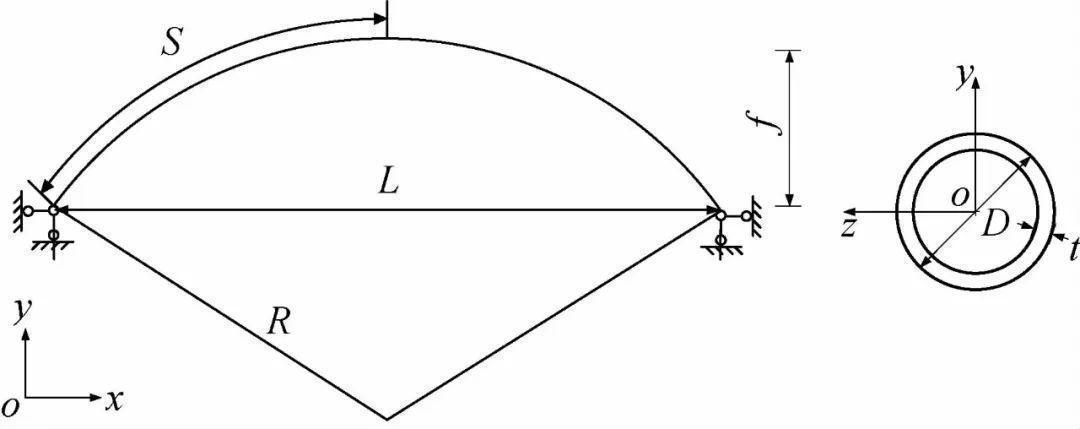
图1 拱结构计算模型（以两铰拱为例）

Fig.1 Arch structure model （e.g.two-hinged arch）

钢管材质为Q345B，材料本构关系采用理想弹塑性模型，屈服强度f_y=345MPa，弹性模量E=2.06×10⁵MPa，泊松比ν=0.30。

HAN等^[14]的研究认为，D/t在14.25~28.50范围内，热弯残余应力与D/t比值之间没有明显的相关性。并且浅拱（f/L＜0.2）对几何缺陷敏感，几何非线性问题严重。因此采用上述一种规格的计算模型进行分析。

采用ABAQUS有限元分析软件，分析中采用C3D8T单元建立几何模型，通过预定义场功能实现残余应力的引入。拱自身的平面外稳定性通过在拱顶和1/4跨处沿z向设置约束来保证。

圆钢管直构件残余应力采用图2a）的分布模型^[15]，残余应力沿管壁厚度方向呈三角形分布，钢管外侧为残余压应力，内侧为残余拉应力，数值均为0.15f_y。

图2 残余应力分布

Fig.2 Residual stress distribution

圆钢管热弯残余应力采用HAN等^[14]的残余应力分布模型，如图2b）所示。在分布模型中，角度α是从起点开始顺时针旋转至测点形成的角度，起点为钢管外壁与中性轴的交点。无量纲化残余应力等于热弯残余应力除以材料的屈服强度。钢管各点处的残余应力由4个关键点K₁、K₂、K₃、K₄控制，其对应的角度分别为90°、160°、200°和270°。热弯残余应力具体数值如表1所示，其中+表示拉应力，-表示压应力。

圆钢管在辊弯过程中同时受到温度和弯矩的作用，使中性轴上部受拉应力，下部受压应力，随后在卸载过程中应力状态受回弹变形和冷却收缩的影响，三者叠加最终得到在中性轴两侧拉压残余应力间隔变化的热弯残余应力分布形式。

2 参数选取

本文考虑拱脚支承形式、荷载形式、长细比3个因素，深入分析了残余应力对圆钢管拱结构平面内极限承载力的影响。其中拱脚支承形式为三种，分别为两拱脚铰接（两铰拱）、两拱脚刚接（无铰拱）和两拱脚水平弹性支承（水平弹性支承拱），如图3所示。水平弹性支承拱的支座刚度与无量纲化的水平弹性柔度系数ξ相关，ξ表征了钢拱截面的抗压刚度与支座刚度的比值。当ξ=0.20时，支座刚度为3.60×10⁷N·m^-1，此时所研究水平弹性支承拱的支座水平位移均小于0.01L，符合工程实际要求^[16]。

图3 拱脚支承形式

Fig.3 Arch supporting forms

荷载形式为四种，分别为跨中集中荷载、1/4跨集中荷载、半跨均布荷载、全跨均布荷载，如图4所示。

图4 荷载形式

Fig.4 Load forms

为了与现有规范进行衔接，在制定纯压钢拱的稳定设计曲线时，借鉴和柱类似的稳定设计思路，采用计算长度系数法，利用钢拱的平面内弹性屈曲系数来进行平面内稳定性设计；引入修正的正则化长细比将不同情况的钢拱进行等效，从而方便制定统一的稳定曲线。长细比的计算方法见式（1）。本文参照文献[10]在0~2范围内选取9种正则化长细比，分别为0.70、0.85、1.04、1.30、1.41、1.50、1.61、1.73、1.84。

式中：λ为拱的几何长细比；S为拱轴轴线长度的一半（图1）；i为圆截面的回转半径。

本文共计对360组圆钢管拱结构模型进行分析。模型命名格式为S_a-Lb-λ_n-resic。a取1表示拱脚铰接，取2表示拱脚刚接，取3表示拱脚弹性支承；b取1表示跨中集中荷载，取2表示1/4跨集中荷载，取3表示半跨均布荷载，取4表示全跨均布荷载；c取0表示无残余应力，取1表示直构件残余应力，取2表示热弯残余应力。

3 极限承载力分析

本文通过有限元分析可获得圆钢管拱结构的平面内极限承载力，如表2所示。其中，N_resi0为无残余应力作用下平面内极限承载力；N_resi1为直构件残余应力作用下平面内极限承载力；N_resi2为热弯残余应力作用下平面内极限承载力；δ₁为引入直构件残余应力后极限承载力的降低幅度；δ₂为引入热弯残余应力后极限承载力的降低幅度。规定：

3.1 拱脚支承形式

本节就不同拱脚支承形式下热弯残余应力对圆钢管拱结构的平面内极限承载力影响进行研究。表2给出了三种拱脚支承形式下钢拱的极限承载力。热弯残余应力对两铰拱极限承载力的最大影响幅度为2.36%；对无铰拱极限承载力的最大影响幅度为1.77%；对弹性支承拱极限承载力的最大影响幅度为1.78%。

由图5可知，在三种拱脚支承形式下，热弯残余应力对钢拱平面内极限承载力的影响与直构件残余应力基本相同，热弯残余应力对钢拱平面内极限承载力的影响不明显。

图5 不同拱脚支承形式的钢拱荷载-位移曲线

Fig.5 Load-displacement curves of steel arches with different supporting forms

3.2 荷载形式

本节就不同荷载形式作用下热弯残余应力对圆钢管拱结构的平面内极限承载力进行研究。

表3给出了四种荷载形式作用下钢拱的极限承载力。热弯残余应力对受跨中集中荷载作用的钢拱的最大影响幅度为2.36%；对受1/4跨中集中荷载作用的钢拱的最大影响幅度为2.59%；对受半跨均布荷载的钢拱的最大影响幅度为1.75%；对受全跨均布荷载作用的钢拱的最大影响幅度为1.78%。

由图6可知，在集中荷载作用下，热弯残余应力对钢拱平面内极限承载力的影响不大。在均布荷载作用下，虽然热弯残余应力对钢拱平面内极限承载力的影响与直构件残余应力相比差别较小，但是热弯残余应力会使拱结构提前进入弹塑性阶段，钢拱在弹塑性过渡区内的承载力会降低。

图6 不同荷载形式下钢拱的荷载-位移曲线

Fig.6 Load-displacement curves of steel arches under different load forms

3.3 不同长细比

本节以在全跨均布荷载作用下的两铰拱和在1/4跨集中荷载作用下的无铰拱为例进行研究。

由图7、图8、图9可知，当长细比较小时（λ_n＜1.30），钢拱达到极限状态时已经进入塑性阶段，钢拱强度得到充分发挥，热弯残余应力对该种情况钢拱极限承载力的影响约为1%；长细比继续增大时（1.30≤λ_n≤1.60），钢拱发生弹塑性稳定破坏，截面只有部分进入塑性阶段，热弯残余应力会使钢拱平面内极限承载力明显降低，最大降幅约为9%；当长细比较大时（λ_n＞1.60），加载过程中钢拱的几何刚度会迅速下降而发生弹性失稳，全截面未进入塑性，从而降低热弯残余应力的影响，极限承载力下降约为3%。

图7 不同长细比的钢拱荷载-位移曲线

Fig.7 Load-displacement curves of steel arches with different slenderness ratios

图8 不同长细比的钢拱Mises应力云图

Fig.8 Mises stress of steel arches with different slenderness ratios

图9 不同长细比对残余应力的影响

Fig.9 Influence of different slenderness ratios on residual stress

热弯残余应力对在1/4跨集中荷载作用下无铰拱平面内极限承载力的影响与在全跨均布荷载作用下的两铰拱情况类似，当长细比较小时（λ_n＜1.40），极限承载力下降约1%；当长细比继续增大时（1.40≤λ_n≤1.70），极限承载力最大降幅约7%；当长细比较大时（λ_n＞1.70），极限承载力下降约1%。

4 结  论

本文基于圆钢管热弯残余应力模型，建立有限元实体模型，考虑拱脚支承形式、荷载形式、长细比3个因素，分析了热弯残余应力对圆钢管拱结构极限承载力的影响。可以得出以下主要结论：

（1）热弯残余应力对两铰钢管拱、无铰钢管拱、水平弹性支承钢管拱平面内极限承载力影响不明显，降低幅度约为2%。

（2）在相同的拱脚约束条件下，当受集中荷载作用时，热弯残余应力对钢管拱平面内极限承载力的最大影响幅度为3%；当受均布荷载作用时，热弯残余应力对钢管拱极限承载力的最大影响幅度为2%，且会使钢管拱提前进入弹塑性阶段。

（3）当λ_n＜1.30时，钢管拱破坏表现为强度破坏，热弯残余应力对钢管拱平面内极限承载力影响为1%；当长细比继续增大时，钢管拱破坏主要表现为弹塑性破坏，热弯残余应力使极限承载力明显下降，最大降低幅度为9%；当λ_n＞1.70时，钢管拱的几何非线性效应明显，钢管拱表现为弹性失稳，热弯残余应力对极限承载力的影响在4%以内。

内容源于网络，如有侵权，请联系删除

相关资料推荐：

钢管拱桁架稳定性及极限承载力研究

圆钢管刚性异形法兰轴拉承载力特性分析及设计方法徐嘉毅

知识点：圆钢管拱结构极限承载力