在《工程力学》中，直梁的弯曲变形是杆件受力变形的基本形式之一，在对梁进行强度和刚度计算时，通常要画出剪力图和弯矩图（即把剪力方程和弯矩方程用函数图像表示出来）以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最大值所在截面的位置。目前，绘制剪力图和弯矩图最常用的规律绘图法中用到一次函数、二次函数和导数等相关知识，这对于数学基础不很扎实的人来说是很难理解的。通过教学，作者在原有绘图方法的基础上，利用选取特殊点代替一次函数、二次函数和导数来绘制剪力图和弯矩图的规律，谨供广大同仁参考。

具体方法为：从上至下依次画出直梁的受力分析图— 特殊截面的剪力值、弯矩值— 剪力图（直角坐标系）—弯矩图（直角坐标系），具体事宜与载荷种类不同有关。

    集中载荷    

例如，图1(a)所示的简支梁 AB 在 C 点处作用集中载荷F，画出此梁的剪力、弯矩图。

首先，求约束反力。画受力图，如图1(a)求支座约束力。

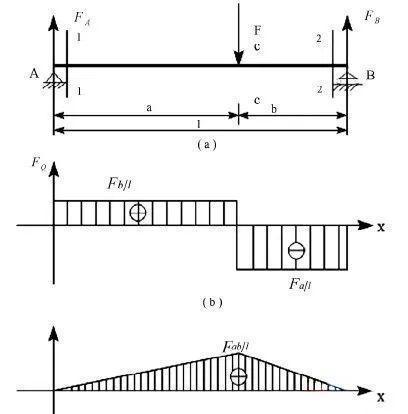
图1 集中载荷作用梁

由平衡方程得：

再画剪力图，如图1(b)。某截面上的剪力即为其截面左（右）段梁上外力的代数和，左上、右下为正，左下、右上为负。AC、CB 段均无载荷作用，剪力图均为水平线。

靠近 A 端的1截面的剪力：

靠近 B 端的2截面的剪力：

在剪力图坐标中画出AC、BC 段的水平线。

最后，画弯矩图，如图1(c)。某截面上的弯矩即为其截面左（右）段梁上外力矩的代数和，左顺、右逆为正，左逆、右顺为负。AC、CB 段无载荷作用，弯矩图为斜直线，确定A、B、C 三点临近截面的弯矩值

在弯矩图坐标中描出A、B、C 三点坐标，分别作出AC、CB 段的斜直线。

    均布载荷    

例如，图2(a) 所示的简支梁 AB 在 C 点处作用均布载荷q，画出此梁的剪力、弯矩图。

图2 均布载荷作用梁

首先，画受力图，如图2(a)。由平衡方程得

再画剪力图，如图(2b)。靠近A点截面上的剪力：

靠近B点截面上的剪力：

在剪力图坐标中描出 A、B 两点，作这两点的连线得剪力图。

最后，画弯矩图，如图2(c)。均布载荷方向向下，弯矩图的形状是抛物线开口向下的抛物线；均布载荷方向向上，弯矩图的形状是抛物线开口向上的抛物线，确定几个特殊点即可画出弯矩图的形状。

靠近 A 点截面上的弯矩：

靠近 B 点截面上的弯矩：

从剪力图中可得剪力为零的点，即为弯矩值最大的点

根据上述三点，画出均布载荷的弯矩图。

    力偶作用    

例如，图3(a)所示的简支梁 AB，在C 点处作用集中力偶MO，试画此梁的剪力、弯矩图。

图3 力偶作用梁

首先，画受力图，如图3(b)。有平衡方程得

再画剪力图，如图3(c)。AC、CB 段无载荷作用，剪力图均为水平线。

靠近 A 端的1截面的剪力：

靠近 B 端的2截面的剪力：

在剪力图坐标中画出 AC、BC 段的水平线。

最后，画弯矩图。AC、CB 段无载荷作用，弯矩图为斜直线，确定A、C^-、C⁺、B点临近截面的弯矩值（C^- 表示在 C 点左侧临近截面；C⁺ 表示C点右侧临近截面）。

在弯矩图坐标中描出 A、C^-、C⁺、B 四点，分别作出 AC^-、C⁺B 段的斜直线。

        结语        

从以上例题中，我们总结出画剪力图和弯矩图的简便方法如下。

• 无载荷作用的梁段上，剪力图为水平线，弯矩图为斜直线。

  
  

• 均布载荷作用的梁段上，剪力图为斜直线，弯矩图为二次曲线。曲线凹向与均布载荷同向，在剪力等于零的截面，曲线有极值。

  
  

• 集中力作用处，剪力图有突变，突变的幅值等于集中力的大小，突变的方向与集中力同向；弯矩图有折点。

  
  

• 集中力偶作用处，剪力图不变；弯矩图突变，突变的幅值等于集中力偶矩的大小，突变的方向，集中力偶顺时针向坐标正向突变，反之向坐标负向突变。

尽管用剪力、弯矩方程能够画出剪力、弯矩图，但应用选取特殊点的简便方法绘制剪力、弯矩图，会更加简捷方便。

内容源于网络，旨在分享，如有侵权，请联系删除

相关资料推荐：

剪力图和弯矩图教程

https://ziliao.co188.com/p63244386.html

知识点：剪力图和弯矩图的快易绘图法