1 引言 强度设计方法(strength design method)中使用的设计假设见于ACI 10.2 中。它们适用于受弯曲、轴向载荷或两者组合的构件设计。钢筋混凝土构件的名义强度(nominal strength)根据这些设计假设来确定。受弯承载力计算时的基本假定包括: (1) 平截面假定; (2) 不考虑混凝土的抗拉强度; (3) 混凝土的本构模型采用简化模型; (4) 钢筋的本构关系采用双直线模型. 这个笔记讨论了与应变相关的假设.
1 引言
强度设计方法(strength design method)中使用的设计假设见于ACI 10.2 中。它们适用于受弯曲、轴向载荷或两者组合的构件设计。钢筋混凝土构件的名义强度(nominal strength)根据这些设计假设来确定。受弯承载力计算时的基本假定包括: (1) 平截面假定; (2) 不考虑混凝土的抗拉强度; (3) 混凝土的本构模型采用简化模型; (4) 钢筋的本构关系采用双直线模型. 这个笔记讨论了与应变相关的假设.
2 平截面假设
强度设计方法的第一个假设是平截面假设. 这个假设基于梁理论中的传统假设: 即弯曲前垂直于弯曲轴的截面在弯曲后仍为平面。在这个假设中, 截面内钢筋和混凝土任一点的应变与该点到中性线(neutral axis)的距离成正比。这称之为应变兼容性(Compatibility of strains)。钢筋的应变等于在该应力水平下混凝土中的应变。这意味着混凝土和钢筋之间有一个完美的粘合,两种材料共同作用,以抵抗外部载荷的影响.
严格地来说,这种假设对于钢筋混凝土构件在开裂后是不正确的,因为由于存在裂缝,中性轴的受拉区应变在任何给定水平上都存在显著差异。不过,许多实验测试已经证实,当在构件的压缩和拉伸区相同长度上测量应变时, 钢筋混凝土的横截面,甚至在接近极限强度情况下,应变的分布基本上是线性的。
必须注意, 对于ACI 10.7中定义的深梁,应变不是线性的,必须利用非线性的应变分布,或者使用规范附录A中概述的支撑连接模型(strut-and-tie model)。
下图显示的是一个矩形钢筋混凝土截面在极限强度下沿着深度的应变分布。假设应变在中性轴以上为压缩应变,在中性轴以下为拉伸应变,混凝土和钢筋的应变与中轴线的距离成正比,中轴线位于截面受压面的c处。
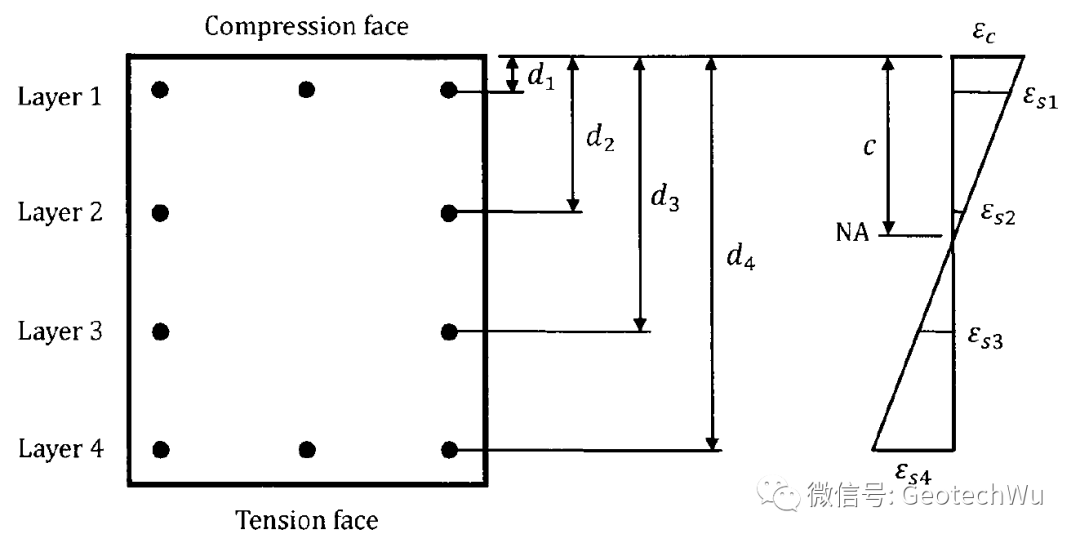
钢筋混凝土截面的假定应变分布
由于应变分布是线性的,因此,在极限压缩纤维处混凝土中的应变ε_c与钢筋中的应变成正比。例如,ε_c与离受压面ε_s4最远的钢筋中的应变之比可以通过相似三角形得到:

ε_c与其他钢筋应变之间也可以建立类似的关系。注意: 最大的拉应变发生在离受压面最远的钢筋上。中性轴线以下的混凝土在极限强度下出现裂缝,从所有意图和目的来看,它不能抵抗任何拉应变, 因此在混凝土的受拉面没有应变。
3 受压区最大可用应变
极限混凝土压缩带的最大可用应变为0.0030。在许多钢筋混凝土构件(梁和偏心载荷柱)和偏心载荷普通混凝土棱柱的压力试验中,已经测出了混凝土破碎时的最大压应变。试验数据在0.0030~0.0080之间变化。最大应变εc=0.0030是一个合理保守的设计建议值.
混凝土压应力达到峰值时的应变和极限压应变的取值,会随混凝土强度等级的不同而有所变化。不同抗压强度的混凝土的应力-应变曲线如下图所示。很明显,与强度较高的混凝土相比,强度较低的混凝土的峰值较长; 还可以看出,与高强度混凝土相比,低强度混凝土的脆性较小,最大应变时断裂的幅度较大。

混凝土压缩试验的应力-应变曲线
大部分中国规范规定受压区极限压应变ε_cu取值为0.0033, 如下图所示. 混凝土弯曲受压时的极限压应变ε_cu的取值如下:当正截面处于非均匀受压时,ε_cu的取值随混凝土强度等级的不同而不同,ε_cu=0.0033-0.5(fcu,k-50)×10^-5,且当计算的值大于0.0033时,取为0.0033;当正截面处于轴心均匀受压时,ε_cu取为0.002。

不同强度级别混凝土受压应力-应变关系模式曲线
4 界限破坏
所谓“界限破坏”,是指正截面上的受拉钢筋的应变达到屈服的同时,受压区混凝土边缘纤维的应变也正好达到混凝土极限压应变时所发生的破坏。此时,受压区混凝土边缘纤维的应变 ε_cu=0.0033-0.5(fcu,k-50)×10^-5,而受拉钢筋的应变ε_x=ε_y=fy/Es。
内容源于网络,如有侵权,请联系删除
相关资料推荐:
诗说混凝土极限压应变
高应变桩基承载力检测
知识点:应变兼容和极限压应变
