边缘构件是剪力墙中重要的组成部分,通过设置边缘构件,能够有效地提高剪力墙的塑性变形能力。 针对剪力墙约束边缘构件,目前主流的配箍(拉)筋方式有两种:一种是采用完全专属于边缘构件的箍筋和拉筋(以下简称“封闭式”,如下图1所示);另一种是采用封闭箍和墙身水平筋隔一布一的形式(以下简称“敞开式”,如下图2所示)。 图1 图2 下面我们针对这两种配箍方式做一个经济性比较,看看哪种方式更省钢筋。需要注意的是,由于一种方式也可计入水平分布筋对体积配箍率30%的贡献。对于“封闭式”配箍,其最终结果“实际体积配箍率”(以下用“ρ
边缘构件是剪力墙中重要的组成部分,通过设置边缘构件,能够有效地提高剪力墙的塑性变形能力。
针对剪力墙约束边缘构件,目前主流的配箍(拉)筋方式有两种:一种是采用完全专属于边缘构件的箍筋和拉筋(以下简称“封闭式”,如下图1所示);另一种是采用封闭箍和墙身水平筋隔一布一的形式(以下简称“敞开式”,如下图2所示)。
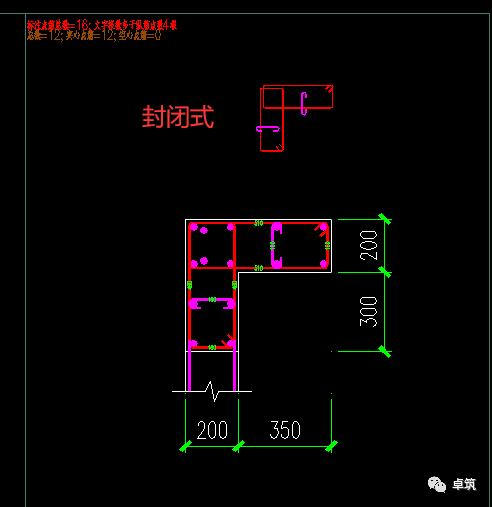
图1

图2
下面我们针对这两种配箍方式做一个经济性比较,看看哪种方式更省钢筋。需要注意的是,由于一种方式也可计入水平分布筋对体积配箍率30%的贡献。对于“封闭式”配箍,其最终结果“实际体积配箍率”(以下用“ρv实”代替)等于边缘构件专属的箍筋/拉筋体积配箍率(以下用“ρv实,1”代替)与伸入边缘构件内的墙身水平分布筋产生的体积配箍率(以下用“ρv实,2”代替)之和(即ρv实=ρv实,1+ρv实,2);对于敞开式配箍,其实际配箍率等于封闭箍层体积配箍率(以下用“ρv实,3”代替),和敞开层(有墙身水平筋)的体积配箍率(以下用“ρv实,4”代替)之和(即ρv实=ρv实,3+ρv实,4)。
在计算前,我们需要先明确几个前提条件及假定:
实际体积配箍率的物理意义是箍筋/拉筋的体积占所约束混凝土体积的百分比,用数学公式表示为:
ρv实=x100%
式中,Ask指箍筋或拉筋的截面面积(mm^2);Lsk指的是箍筋及拉筋的总长度(mm)(注:重叠部分长度值计入一次);Acor指的是最外层箍筋包裹(约束)的混凝土的总面积(mm^2);S表示箍筋及拉筋的间距(mm)。
假设保护层厚度c均为15mm。
为方便手算,箍筋及拉筋的倒角全部视为直角,弯钩全部忽略不计。
我们以某剪力墙高层住宅项目的二至四层墙柱配筋图为例。从中选取两个具有代表性的的约束边缘构件,用上述两种配箍方式分别计算其体积配箍率。

本工程地下两层,地上34层,其中约束边缘构件层从基础顶到5层楼面(所以二至四层墙柱为约束边缘构件层),抗震等级及抗震构造措施的等级均为二级。约束边缘构件的最小体积配箍率ρv,min与混凝土强度等级、钢筋强度等级及剪力墙的墙肢轴压比,抗震构造措施的等级等因素有关。按《高规》7.2.13、7.2.14、7.2.15的相关要求,可以得出以下结论:
箍筋最小体积配箍率:当0.3<μ≤0.4时,ρv,min=0.843%;
箍筋最小体积配箍率:当0.4<μ≤0.6时,ρv,min=1.406%;
箍筋最小体积配箍率:当0<μ≤0.3时,配构造边缘构件,纵筋取0.8%AC与6φ14的较大值,箍筋不小于φ8@150。
算例1:YBZ13

计算书

封闭式

敞开式
由于轴压比μ为0.45>0.4,所以该边缘构件的构造最小体积配箍率ρv,min为1.406%。
下面分别计算两种配箍方式的实际配箍率。
封闭式:
ρv实,1=
(78.5x(200-15x2-10)x7+(750-15x2-10)x2+(850-15-10/2)x2)/(206250x130)x100%=329700/26812500=1.23%
ρv实,2=[50.3x(850-15-8/2)x2]/(206250x200)=0.203%
ρv实=1.23%+0.203%=1.433%>1.406%,满足构造要求,且实际配箍率比构造配箍率大1.9%。
敞开式:
ρv实,3=
(78.5x(200-15x2-10)x7+(750-15x2-10)x2+(850-15-10/2)x2)/(206250x200)x100%=329700/41250000=0.799%
ρv实,4=
(78.5x(200-15x2-10)x7+(750-15x2-10)x2)+50.3x(850-15-8)x2)/(206250x200)=283089.2/41250000=0.686%
ρv实=0.799%+0.686%=1.485%>1.406%,满足构造要求,且实际配箍率比构造配箍率大5.6%。
另外,墙身水平筋所提供的体积配箍率为:
50.3x((850-15-8/2)x2)]/(206250x200)=0.202%
墙身水平筋占边缘构件的构造体积配箍率为:0.202%/1.406%=14.4%<30%。
算例2:YBZ5

计算书

封闭式

敞开式
由计算书可知,该边缘构件墙肢轴压比大于0.4,故构造最小配筋率为1.406%。
封闭式:
ρv实,1=
[78.5x((200-15x2-10)x4+(550-15x2-10)x2+(500-15-10/2)x2)]/(123750x130)=205670/17325000=1.28%
ρv实,2=[50.3x(500-15-8/2)x2]/(123750x200)=0.196%
ρv实=1.21%+0.202%=1.476%>1.406%,满足构造最小体积配箍率要求,且实际配箍率比构造配箍率大4.9%。
敞开式:
ρv实,3=
[78.5x((200-15x2-10)x2+(550-15x2-10)x2+(500-15-10/2)x2)+50.3x(200-15x2-8)x2]/(123750x200)=199987.2/24750000x100%=0.808%
ρv实,4=
[78.5x((200-15x2-10)x1+(550-15x2-10)x2)+50.3x((200-15x2-8)x3+(500-15-8/2)x2))]/(123750x200)=168705/24750000x100%=0.682%
ρv实=0.808%+0.682%=1.49%>1.406%,满足构造最小体积配箍率要求,且实际配箍率比构造配箍率大5.9%。
另外,墙身水平筋所提供的体积配箍率为:
50.3x((500-15-8/2)x2)]/(123750x200)=0.196%
墙身水平筋占边缘构件的整体体积配箍率为:0.196%/1.406%=13.9%<30%。
算例3:YBZ1

计算书

封闭式

敞开式
由计算书可知,该边缘构件墙肢轴压比大于0.4,故构造最小配筋率为1.406%。
封闭式:
ρv实,1=
[50.3x((400-15-8/2)x2+(200-15x2-8)x3]/(58058x100)=62875/5805800=1.08%
ρv实,2=[50.3x(400-15-8/2)x2]/(58058x200)=0.33%
ρv实=1.08%+0.33%=1.41%>1.406%,满足构造最小体积配箍率要求,且实际配箍率几欲全权相等。
敞开式:
ρv实,3=
[113x((400-15-8/2)x2+(200-15x2-8)x2)+50.3x(200-15x2-8)x1]/(58058x200)=131092.6/5805800=1.13%
ρv实,4=
[50.3x((400-15-8/2)x2+(200-15x2-8)x3]/(58058x200)=62705/24750000x100%=0.541%
ρv实=1.13%+0.541%=1.671%>1.406%,满足构造最小体积配箍率要求,且实际配箍率比构造配箍率大18.8%。
另外,墙身水平筋所提供的体积配箍率为:
50.3x((400-15-8/2)x2+(200-15x2-8)]/(58058x200)=0.4%
墙身水平筋占边缘构件的整体体积配箍率为:0.4%/1.406%=28.4%<30%。
综合以上三个算例可以看出:由于封闭式配箍不受墙身分布筋竖向间距的影响,配箍方式更灵活多样,所以可以得到更接近构造最小配箍率的配箍方案。而“敞开式”配箍受限于墙身水平筋间距的要求,导致其整体体积配箍率不太好人为控制(有时偏大,造成一定的钢筋浪费;有时偏小,不满足最小配箍率的要求,其呈现出的变化规律是:边缘构件的投影面积越小,墙身水平筋的占比越大,而整体体积配箍率超出值越多。),综上所述,“封闭式”配箍是更优的配箍方式。
内容源于网络,如有侵权,请联系删除
相关资料推荐:
剪力墙约束边缘构件体积配箍率及核心区面积计算
剪力墙边缘构件的体积配箍率计算表格
知识点:剪力墙边缘构件体积配箍率
