先说结论：
1、梁格法计算结果与梁格划分有关，存在一定主观性，使用时需要注意。
2、中载布载情况下，梁格法、剪力流法、坐标法计算结果接近。
3、偏载布载情况下，由于梁格法无法考虑箱梁扭转，扭转通过各片梁弯曲来平衡，因此边、中腹板剪力差别最大；坐标法与剪力流法中腹板计算结果接近，边腹板计算结果存在差别，考虑坐标法与支承位置关系密切，其计算结果更适用于支承位置；剪力流法与支承位置无关，其计算结果更适用于跨中无支承位置。

一、现浇箱梁计算模型概述
对于混凝土现浇箱梁计算分析，通常设计采用单梁模型进行，较少采用板壳单元或实体模型，主要原因是板壳单元或实体单元建模一般采用通用有限元软件完成，建模过程复杂，考虑混凝土收缩徐变、预应力钢束摩阻损失等极为不便。单梁模型建模容易，适用于不断调整的设计过程，缺点是无法考虑空间效应，比如箱梁的横向分布，即在一定载荷作用下，箱梁各部分受力的不均匀情况，无法用单梁模型进行分析，为此2018桥规提出了3种方法：①空间网格模型；②折面梁格模型；③7自由度梁单元模型。对于箱梁横向分布，即一定载荷下箱梁各腹板剪力分配，还有其他方法，比如剪力流法、坐标法等，本文重点对2018桥规梁格法、剪力流法、坐标法进行对比分析。

二、各种方法简介
（一）空间网格模型
空间网格模型是对实际箱梁结构进行逐级简化得出，其简化路径为实际结构→离散为板件→板件用十字交叉纵横梁代替。
对于现浇箱梁而言，该模型仍然是整体框架，能够反映出空间效应的分布规律。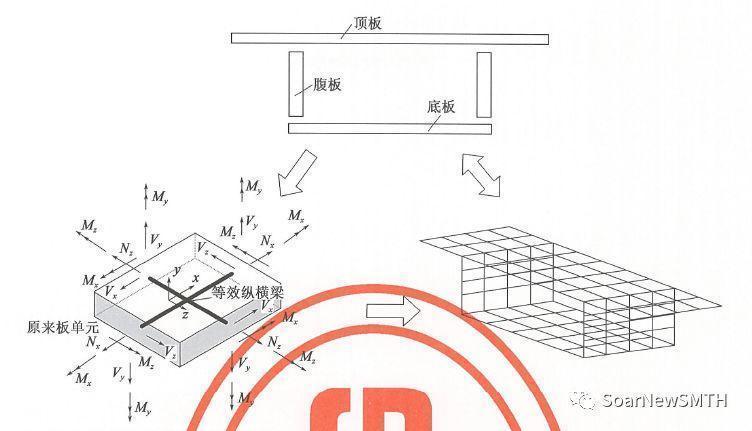


（二）折面梁格模型
折面梁格模型，是按照一定划分原则，直接将箱梁横向划分为多梁。梁格模型存在如下问题：①划分具有一定的主观性，求算腹板剪力时，需要将无腹板单梁“剪力”折算进来，实际上顶、底板并不存在向下的剪力，其剪力流方向与板件方向相同；②箱梁为闭口截面，抗扭刚度较大，而多梁为多根开口截面梁的组合，每根梁的抗扭刚度很小，截面整体扭矩通过各片梁受弯来平衡，这会造成偏载作用下，腹板剪力效应失真。


（三）7自由度单梁模型
通常的空间梁单元是6自由度，包括一个端点的XYZ位移，梁体三个方向的转动。其内力包括轴力、剪力、弯矩和扭矩，不考虑截面翘曲，即不考虑约束扭转产生的截面正应力。7自由度梁单元，在6自由度梁单元基础上，考虑截面翘曲效应，引入约束扭转系数，进行约束扭转状态下的截面正应力和剪应力计算。

（四）剪力流法
开口截面梁各板件剪力流分布是静定问题，根据截面应力平衡，即可求出各板件剪力流分布。箱梁为闭口截面梁，各板件剪力流分布是超静定问题，仅根据截面应力平衡无法求解，需要引入变形协调条件进行求解，详见参考文献1和2。


（五）坐标法
坐标法是笔者在2012年前后设计类板式箱梁时提出的。类板式箱梁通常宽度较大，支承间距也大，箱梁整体受力特性偏向于板，基于越靠近支承位置剪力越大的事实，直接构建剪力分布函数，对各腹板区段进行积分，得到其剪力。


三、梁格法不同划分方法计算对比
梁格法的计算结果与梁格的划分有关，下面举例说明。

如图所示，对同样尺寸的单箱3室箱梁，均按照规范要求，采用两种划分方式，第一种划分为7片梁，第二种划分为3片梁，在同样位置进行2车道布载，按偏心压力法计算各片梁的横向分布系数，即各片梁的剪力分配，结果如下：



由计算结果可见，不同划分方式下，各片梁横向分布结果不同。采用7片梁时，各腹板梁分配系数较小，如将无腹板梁承担的“剪力”均分至腹板梁，则结果与3片梁模式接近。实际上无腹板梁中，箱梁断面上，顶、底板剪力流方向与板件平行，并不存在向下的剪力。

四、梁格法、剪力流法、坐标法计算对比
本次采用四种结构进行对比：①桥宽17m、单箱3室有悬臂箱梁；②桥宽13m、单箱3室无悬臂箱梁；③桥宽12.5m、单箱2室有悬臂箱梁；④桥宽8.5m、单箱2室无悬臂箱梁。如图所示：
载荷分偏载、中载两种工况，分别采用梁格法、剪力流法、坐标法计算进行对比，其中梁格法采用上述第2种模式，即尽可能扩大有腹板梁范围，减小无腹板梁范围。

各腹板剪力分配值计算结果如下表所示，由表可见：
1、中载情况下，剪力流法、梁格法、坐标法3种方法计算结果接近；
2、偏载情况下，3种方法计算结果差别较大。
1）梁格法无法考虑扭转刚度，扭转通过各片梁弯曲来平衡，所以边腹板剪力差别最大，中腹板剪力与其他两种方法差别大；
2）坐标法与支承位置关系密切，如图所示的支承位置，边腹板距支承位置近，中腹板距支承位置远，所以边腹板剪力差别最小，中腹板剪力与剪力流法计算结果接近；
3）剪力流法分别考虑弯曲剪力流和扭转剪力流，组合得到各腹板剪力分配结果，边腹板剪力差别居中；中腹板剪力与坐标法计算结果接近。





五、结论
1、梁格法计算结果与梁格划分有关，存在一定主观性，使用时需要注意。
2、中载布载情况下，梁格法、剪力流法、坐标法计算结果接近。
3、偏载布载情况下，由于梁格法无法考虑箱梁扭转，扭转通过各片梁弯曲来平衡，因此边、中腹板剪力差别最大；坐标法与剪力流法中腹板计算结果接近，边腹板计算结果存在差别，考虑坐标法与支承位置关系密切，其计算结果更适用于支承位置；剪力流法与支承位置无关，其计算结果更适用于跨中无支承位置。

内容源于网络，如有侵权，请联系删除

相关资料推荐：

分体式箱梁桥荷载横向分布计算方法

https://ziliao.co188.com/p48068553.html

知识点：箱梁横向分布计算