一、无梁楼盖中混凝土柱的设计 运用PKPM进行无梁楼盖设计 方法1、用等代梁的方法。等代楼宽度在竖向荷载作用下取相邻跨各1/2(水平荷载作用下取1/4),板厚为0,重叠的梁自重应作相应扣除。 方法2、用虚梁+弹性板6的方法。 不同程序及计算模型下柱内力结果 l 计算模型:X向轴网间距为3500,8100X5,2400 Y向轴网间距为8100X4,无梁楼盖板厚为400,四周为300厚砼外墙。梁、板砼为C30,墙、柱为C35,恒载为60kN/m**2 ,活载2kN/m**2。
一、无梁楼盖中混凝土柱的设计
运用PKPM进行无梁楼盖设计
方法1、用等代梁的方法。等代楼宽度在竖向荷载作用下取相邻跨各1/2(水平荷载作用下取1/4),板厚为0,重叠的梁自重应作相应扣除。
方法2、用虚梁+弹性板6的方法。
不同程序及计算模型下柱内力结果
l 计算模型:X向轴网间距为3500,8100X5,2400 Y向轴网间距为8100X4,无梁楼盖板厚为400,四周为300厚砼外墙。梁、板砼为C30,墙、柱为C35,恒载为60kN/m**2 ,活载2kN/m**2。
l (由于跨度及边支座不同的原因,主要考虑边柱恒载作用下的弯矩)
Etabs,3轴西侧边柱柱顶X向弯矩:431.07kN.m
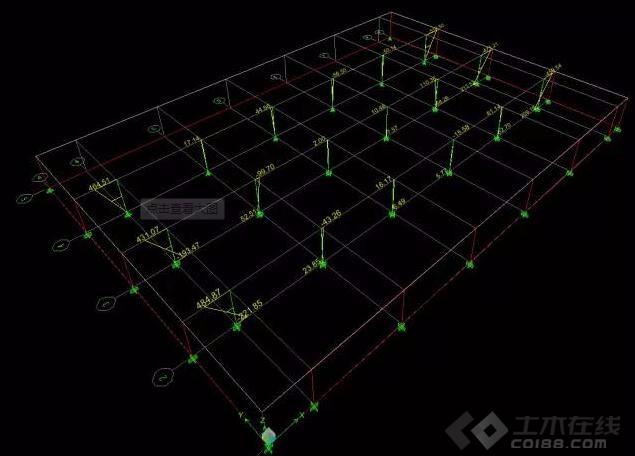
Midas,3轴西侧边柱柱顶X向弯矩:421.19kN.m

SATWE中8.1m等代梁,3轴西侧边柱柱顶X向弯矩:609.6kN.m

SATWE中柱间设虚梁,3轴西侧边柱柱顶X向弯矩:848.9kN.m

SATWE1m间距虚梁,3轴西侧边柱柱顶X向弯矩:447.7kN.m

SATWE边跨及相邻跨1m,其它跨8.1m间距虚梁,3轴西侧边柱柱顶X向弯矩:487.1kN.m

Etabs考虑柱帽3.2X3.2X0.4,3轴西侧边柱柱顶X向弯矩:299.9kN.m

上述结果汇总
分析结果讨论:
1、Etabs和Midas程序的内力计算模型均是板上荷载通过板单元节点,并最终传导到柱上,与实际情况相符,且两者计算结果相近,可认为基本正确。
2、SATWE程序的内力计算模型是先将荷载导算到梁上,再通过梁传导到柱上,且板、梁间节点位移不协调,因而柱间虚梁模型与实际结果相差较大。等代梁模型是一种简化模型,计算结果相差也较为明显。
3、按1m间距布虚梁后,其内力计算模型与Etabs和Midas相近,计算结果也相差不大。在不等间距的边跨和相邻跨按1m布虚梁后的结果也可接受。如采用SATWE程序,实际计算中可采用这二种方式中的一种进行建模计算。
4、考虑柱帽后柱顶弯矩有一定程度的减小,简化计算时可作为安全储备而不作考虑。
不同条件下无梁楼盖各顶经济指标
l 建 筑条件:3m覆土,8.1m柱网。不同条件下的各项经济指标。注:普通混凝土顶板顶部按0.2,底部按0.3mm裂缝宽度进行控制,按新版混凝土规范计算 公式。顶部跨中按支座部分的钢筋一半拉通考虑,底部全部拉通,预应力按无裂缝控制。计算中仅取五连跨的中间跨进行计算,即计算面积取8.1X8.1,折合 钢筋用量时,预应力筋取普通筋的2倍,预应力构件中混凝土普通钢筋按最新规范取为0.2%
托板为3.2X3.2X0.4,平板为0.4m时各项指标
托板为3.2X3.2X0.4,平板为0.45m时各项指标
托板为3.2X3.2X0.6,平板为0.4m时各项指标
覆土条件为2m.板为3.2X3.2X0.4,平板为0.35m时各项指标
覆土条件为2m.托板为3.2X3.2X0.4,平板为0. 4m时各项指标
当托板改为600厚,平板350时,单方钢筋含量变为:37.45
上述结果最终结果汇总(折合普通筋单方含量)
基本结论及相关问题
一、基本结论
1、对于覆土在2m以上的情况,由于增加板厚对内力影响不大,对配筋影响很大,故板厚不能太小,覆土越厚,增加板厚越经济。
2、由于支座处内力较大,在建筑许可的条件下尽可能增加托板厚度,对普通混凝土楼盖经济效果显著。
3、一般情况下,预应力混凝土楼盖较普通混凝土楼盖更为经济。由于预应力钢筋一般采取通长的形式,其数量可能由跨中板带决定,因而托板厚度对其影响不明显。通过比较,当托板增加到一定厚度时,预应力砼楼盖经济性与普通混凝土相当。
二、问题1、等代框架法与有限元法计算的总弯矩差异问题。
2、有限元计算结果与经验分配系数问题
SAFE 有限元计算结果与SLABCAD结果接近。根据上述可知,总弯矩相差不是很大,但并不是按柱上板带支座处按0.75:0.25进行分配,而是接近 0.89:0.11;支座与跨中更不是2:1 而是接近4:1。对于无柱帽的无梁楼盖,通过有限元分析可得到接近0.75:0.25及2:1的经验结果,在用理正计算时应该注意,对于有柱帽的情况不宜 直接采用默认的分配系数。
3、理正工具箱支座计算截面的高度问题
理正工具箱对于有柱帽的结构采用的经验算法,即折梁跨度的算法,因而支座内力与折减后的跨度的端部对应,而不是柱边截面。对应的应该是柱边往外2/3C处的位置,因此截面设计时应采用此处的截面高度,采用锥形柱帽时应该注意。
4、正反柱帽对预应力筋配筋影响问题
预应力结构设计中最为复杂的二点是:一是计算预应力损失。二是求解预应力次内力。
幻灯片24
在 手算过程中这二步常会被简化考虑。预应力损失通常取张拉控制应力的25~30%;而次弯矩常会按支座有利,跨中不利来考虑,前面的计算结果即是支座按 -5%,跨中按12%的标准组合弯矩进行考虑.通常情况,尤其是对于预应力大梁的情况,上述经验值与实际情况出入不大,但对于预应力楼盖的情况可能不符。
同样是对于上述五跨连续梁3m覆土的情况,正柱帽与反柱帽的预应力布筋如下图所示:两者矢高明显不同,所产生的等效荷载不同,最终导致次弯矩不同。
当反弯点取在0.15L处时,其单根预应力效应及相应的预应力配筋分别如下表所示:单位为kN或kN.m或kN/m
好技能,Get!
