知识点:分数槽永磁同步电机 1 电机基本参数及模型 常规均匀气隙的内置式PMSM,转子结构的形状为以点O为圆心的圆形。为了改善电机气隙磁场磁密波形,在永磁体一个极距范围内,以O′为转子外圆的圆心,结构如图1所示,用偏心距dm=OO′的长度来衡量电机气隙非均匀程度。 图1 内置式PMSM非均匀气隙结构图 样机主要参数如表1所示,根据样机参数建立的二维电磁计算模型如图2所示。
知识点:分数槽永磁同步电机
1 电机基本参数及模型
常规均匀气隙的内置式PMSM,转子结构的形状为以点O为圆心的圆形。为了改善电机气隙磁场磁密波形,在永磁体一个极距范围内,以O′为转子外圆的圆心,结构如图1所示,用偏心距dm=OO′的长度来衡量电机气隙非均匀程度。
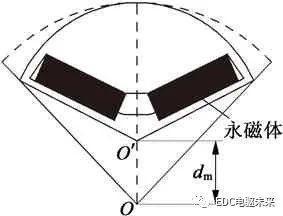
图1 内置式PMSM非均匀气隙结构图
样机主要参数如表1所示,根据样机参数建立的二维电磁计算模型如图2所示。
表1 样机主要参数


图2 样机基本模型
2 电机电磁力波的分析
2.1 电磁力波特性分析
在不考虑饱和与铁心磁阻的影响情况下,内置式PMSM气隙磁场正弦电流供电时,气隙磁密的解析表达式:
b(θ,t)=f(θ,t)Λ(θ)=[∑fμ(θ,t)+∑fv(θ,t)]·
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1)
式中:∑fμ(θ,t)为转子永磁体谐波磁动势;∑fv(θ,t)为定子绕组谐波磁动势;Λ(θ)为相对磁导函数;μ为转子磁场谐波次数;v为定子磁场谐波次数;ω为基波磁势角频率;p为电机极对数;z为电机槽数。
去除切向磁通密度的影响,由麦克斯韦应力张量方程可知,径向电磁力波的瞬时值在单位面积上解析表达式[19]:
![]()
![]()
ppm+ppm-s+ps
(2)
式中:b(θ,t)为径向气隙磁密;μ0为真空磁导率,μ0=4π×10-7 H/m;ppm为转子磁场之间互相作用引起的电磁力密度;ps为定子磁场之间互相作用引起的电磁力密度;ppm-s为转子磁场与定子磁场互相作用引起的电磁力密度。
PMSM径向力波的空间力波阶数r与电机极对数和槽数有关。电磁力波引起的振动与力波幅值呈正比,与力波阶数r的4次方呈反比,因此在计算电机的振动时,可以忽略高阶力波的影响[20]。根据前文理论分析结果,可以得到电磁力波在转子磁场之间互相作用、转子磁场与定子磁场互相作用两种情况下的各频谱分量和谐波来源,如表2和表3所示。
表2 6槽4极电机转子磁场之间互相作用电磁力波来源表

表3 6槽4极电机转子磁场与定子磁场互相作用电磁力波来源表

表2、表3中![]() 为定子基波频率,n为电机转速,p为电机极对数,z为电机槽数。
为定子基波频率,n为电机转速,p为电机极对数,z为电机槽数。
根据表2和表3可知,r=2、4阶为6槽4极PMSM的空间径向电磁力波的主要阶数,其中r=2阶电磁力波的力波频率主要有4f,10f,16f,22f,…;r=4阶电磁力波的力波频率主要有2f,8f,14f,20f,…。
分析表2可得,转子基波磁场和转子磁场3次、5次磁密谐波是产生样机转子磁场互相作用r=2阶电磁力波的4f与r=4阶电磁力波的2f的主要谐波次数。
分析表3可得,转子磁场3次、5次磁密谐波和定子基波磁场、2次、4次磁密谐波是产生样机电枢反应r=2阶电磁力波的4f的主要谐波次数;转子基波磁场、3次磁密谐波和定子基波磁场、2次、4次磁密谐波是产生样机电枢反应r=4阶电磁力波的2f的主要谐波次数。
2.2 气隙磁场有限元分析
利用有限元软件建立6槽4极非均匀气隙PMSM二维电磁模型,仿真计算出样机在额定转速下的空载和负载气隙磁通密度,并在某一时间下对其进行傅里叶级数分解,得出气隙径向磁通密度及其傅里叶级数分解,如图3所示。

(a) 径向磁通密度

(b)径向磁通密度傅里叶级数分解
图3 某一时刻气隙径向磁通密度及其傅里叶级数分解
由图3可知,径向磁通密度包含大量的谐波,次数较大的有3次、5次。负载工作点相对于空载工作点,各次谐波幅值均增大,谐波之间相互作用可能产生较大的电磁力波,和空载时相比会引起更大的振动噪声。
3 多物理场电磁振动仿真计算
图4为本文PMSM电磁场和结构场耦合电磁振动仿真计算流程图。首先建立用于电磁力计算的电磁有限元模型,然后建立电机定子的结构有限元模型,把二维电磁场计算得到的电磁力加载到三维电机定子结构上,计算定子振动的响应频谱特性,最后测试样机的振动特性,验证有限元仿真结果。

图4 电机电磁振动仿真计算流程图
3.1 电磁力波仿真分析
采用瞬态有限元方法对样机进行分析计算,得到气隙磁场与定子铁心相互作用产生的电磁力密度,如图5所示。仿真计算出样机在额定转速下的空载和负载径向电磁力,并对其进行空间上的傅里叶级数分解,结果如图6所示。

图5 定子齿径向力密度
由图6可知,样机的空间径向电磁力波的阶数主要是r=2阶、r=4阶、r=6阶等,造成电机电磁振动的主要原因为低阶电磁力波的存在,对于6槽4极PMSM,r=2阶径向电磁力波是造成电机电磁振动的主要原因。负载时各阶电磁力波的幅值都增加,r=2阶的幅值增加了22%,因此电机负载时的振动噪声加剧。电机运行在负载情况下,会发生电枢反应,造成电机相对于空载运行时的电磁力波幅值增大。该结果与电磁力波解析法分析结果一致。

(a) 径向电磁力

(b) 径向电磁力傅里叶级数分解
图6 空间上径向电磁力及其傅里叶级数分解
图7为电机运行在额定转速下,电机内部齿中心处的一点在时间变化上径向电磁力的波形及其傅里叶级数分解结果。

(a) 径向电磁力

(b)径向电磁力傅里叶级数分解
图7 时间上径向电磁力及其傅里叶级数分解
由图7可知,径向电磁力波的时间频率是2f,4f,6f,…,其中2f分量的幅值远远大于其它谐波分量。由表2和表3可知,电磁力波的2f分量主要由基波产生,因此幅值比较大;和空载时相比,负载时各谐波分量的幅值增加。这是因为空载时转子磁场相互作用产生径向力波谐波分量,负载时电磁力谐波除了转子磁场相互作用产生外,定转子磁场相互作用也会产生大量的电磁力谐波,有限元结果验证了前文的理论分析结果。
3.2 样机模态分析
对电机进行固有模态特性分析,设计电机时尽量使电机定子的固有频率避开径向电磁力波的高频频率,避免发生结构共振,是抑制电机电磁振动噪声的关键。对电机定子铁心进行模态分析,定子铁心密度为7 410 kg/m3,弹性模量为206 GPa,泊松比为0.3,定子铁心三维有限元仿真模型与网格剖分图如图8所示。

(a) 三维有限元模型

(b)网格剖分图
图8 定子铁心三维有限元仿真模型与网格剖分图
图9为样机定子铁心模态振型与模态频率仿真结果。

(a) n=2 f=2 015 Hz

(b) n=3 f=4 611 Hz

(c) n=4 f=8 930 Hz

(d) n=5 f=11 690 Hz
图9 样机定子结构有限元振动模态
3.3 多物理场电磁振动频谱分析
建立电磁场和结构场的耦合模型。将电磁力施加到电机定子齿内表面上,得到电机的电磁振动响应频谱特性,如图10所示。

(a)有限元仿真响应频谱

(b) 2 020 Hz处振型

(c)8 940 Hz处振型
图10 样机电磁振动有限元响应频谱及形变观测图
由图10可知,定子铁心在2f=340 Hz,4f=700 Hz,2 020 Hz,8 940 Hz处均发生了明显的振动。
由前文分析得到的径向电磁力成分可知,频率为2f,4f的径向电磁力幅值大,在这些频率下电机振动明显。
频率在2 020 Hz,8 940 Hz处对应的振动加速度幅值相对较大,分别与电机2015Hz(n=2)、8 930 Hz(n=4)的固有频率接近,振动加速度的幅值分别为3.559 m/s2、0.867 m/s2,其中,二阶固有频率处的振动加速度最大,但由于2 020 Hz=12f、8 940 Hz=52f,该两频率下的电磁力幅值相对较小,不会引起较大的共振。
综上,径向电磁力幅值较大时所对应的频率,远离电机各阶模态所对应的固有频率,本文样机的固有频率避开了电磁力较大的力波阶数的频谱,有限元仿真结果表明,该电机振动幅值较小,不会辐射较大的振动噪声。
4 样机振动实验测试
为了验证前文的分析结果,实验测试样机的振动特性。实验测试图如图11所示,其中,使用的动态数据采集分析仪型号为AVANT MI-7008,最大采样频率为204.8 kHz;ICP型三向加速度传感器采集信号,灵敏度100 mV/g;负载为磁粉制动器。

图11 样机振动实测图
图12为额定工况下电机运行在5 200 r/min时径向振动加速度与实测结果的对比。从图12中可看出,仿真计算与实验测量在2 000 Hz和8 900 Hz附近有较大的振动,验证了仿真结果的正确性。实测振动响应频谱波形波动较大,这是由于电机振动实验中是整机,而仿真计算仅研究了样机的定子铁心结构,因此实验结果与计算结果有误差。

图12 样机仿真计算电磁振动与实测结果对比
5 结 语
本文引入了一种分数槽PMSM振动频谱特性和振动源的分析方法,理论分析了PMSM电磁力波的产生原理和各阶力波的谐波来源,对一台6槽4极非均匀气隙PMSM建立了电磁场和结构场多物理场耦合有限元模型,分析了电机电磁振动特性,并进行了实验验证。仿真与实验结果表明,对于本文6槽4极样机,样机各阶固有频率远离引起电机共振的力波频率,运行过程中不会发生较大的共振。本文方法也适用于其他极槽配合电机的振动频谱特性和振动源的分析。
相关推荐:
