(1)交叉基础荷载分配计算的原则 当上部荷载较大、地基土较软弱,只靠单向设置柱下条形基础已不能满足地基承载力和地基变形要求时,可采用沿纵、横柱列设置交叉条形基础,又称十字交叉梁基础。 ↑交叉基础示意图 柱下十字交叉条形基础在基础交叉点处承受柱网传下的集中荷载和力矩。十字交叉条形基础梁的计算较复杂,一般采用简化计算方法。通常把柱荷载分配到纵横两个方向的基础上,然后分别按单向条形基础进行内力计算。
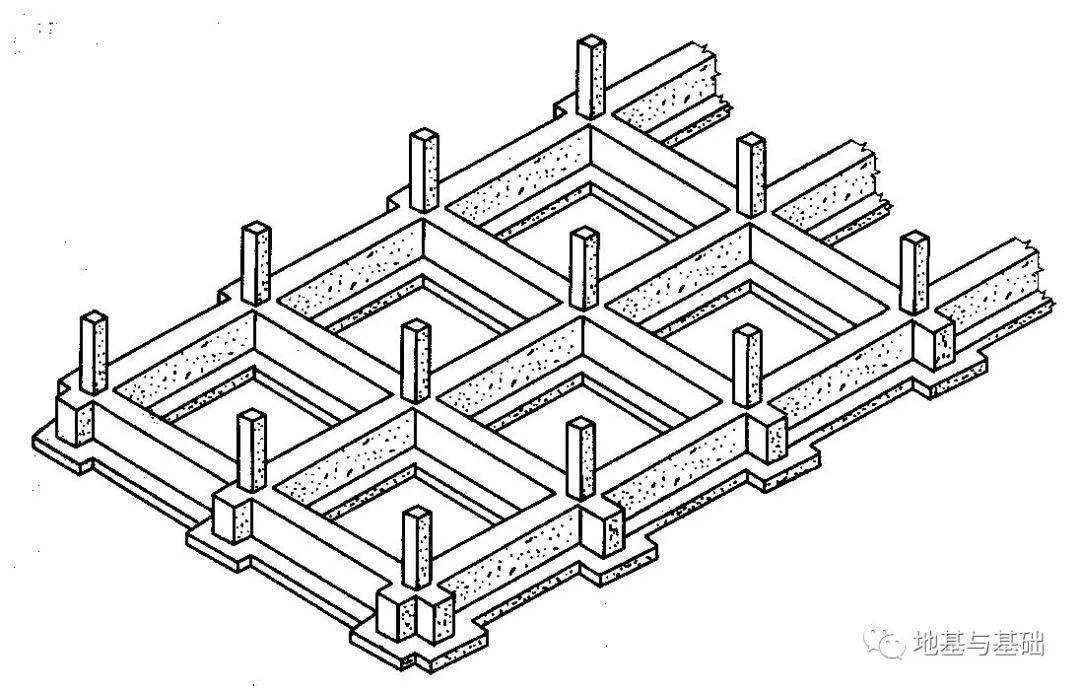
↑交叉基础示意图
柱下十字交叉条形基础在基础交叉点处承受柱网传下的集中荷载和力矩。十字交叉条形基础梁的计算较复杂,一般采用简化计算方法。通常把柱荷载分配到纵横两个方向的基础上,然后分别按单向条形基础进行内力计算。

其计算主要是解决节点荷载分配问题,一般是按刚度分配或变形协调的原则,沿两个方向分配。下面简要讨论。节点荷载分配,不管采用什么方法,都必需满足两个条件:

按地基与基础共同作用的概念,则纵横基础梁在节点i处的竖向位移和转角应相同,且应与该处地基的变形相协调。简化计算方法假定交叉点处纵梁和横梁之间铰接,认为一个方向的条形基础有转角时,对另一个方向的条形基础内不引起内力,节点上两个方向的力矩分别由对应的纵梁和横梁承担。这样,只要满足节点处的竖向位移协调条件即可。即:

按以上原则进行荷载分配显然很复杂,必须做适当简化,因为只有求得弹性地基上梁的挠度才能给出节点位移,而此时两组梁上的荷载是待定的,因此,必须把柱荷载的分配与两组弹性地基梁的内力与挠度联合求解。为简化计算,一般采用文克尔地基模型,略去其它节点的荷载对本结点挠度的影响。
柱节点分为三种:中柱节点、边柱节点和角柱节点。对中柱(内柱)节点,两个方向的基础可看做
无限长梁
;对边柱节点,一个方向基础视为无限长梁,而另一方向基础视为
半无限长梁
;对角柱节点两个方向基础均视为半无限长梁。

对中柱(内柱)节点,两个方向的基础可看做无限长梁,作用点的位移表达式为





(3)节点荷载分配的调整
按照以上方法进行柱荷载分配后,可分别按两个方向的条形基础计算。但这种计算,在交叉点处基底重叠面积△A重复计算了一次,结果使地基反力减少,致使计算结果偏于不安全,故按上述节点荷载分配后还需进行调整。
知识点:柱下十字交叉条形基础的荷载分配










