1 引言

剪力墙洞口连梁的跨度较小,竖向荷载引起的弯矩所占比例很小。除承受少量重力荷载引起的弯矩作用外,主要承受水平地震与风荷载作用产生的弯矩与剪力。水平荷载作用的反弯点位于跨中,各截面所受剪力基本相同。为了实现“强剪弱弯”使连梁具有一定的延性,对于深连梁给出了连梁剪力设计值的增大系数。跨高比小于 2.5 的剪力墙连梁,在进行抗震设计时,为了降低地震剪力,采用较大幅度的连梁刚度折减以降低连梁的作用剪力。在高层建筑框架-剪力墙结构或框架-核心筒结构中,当剪力墙长度过大时存在的问题较多:墙体刚度过大,受力集中,墙体高宽比较小,结构抗震延性差,且与框架的剪力分配不合理。连梁受截面抗剪承载力控制,减小刚度将带来抗侧力刚度的不足。

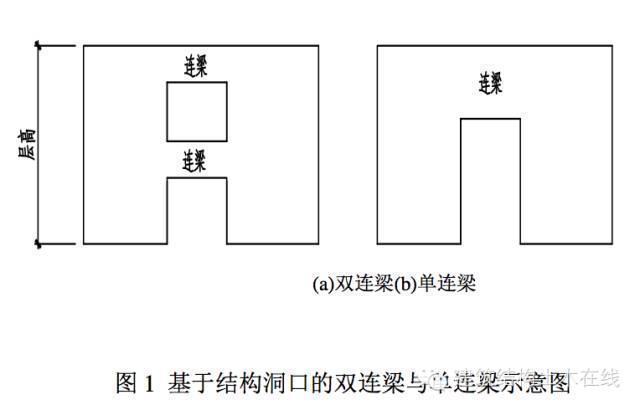
本文提出的双连梁是在同一楼层高度内,沿高度方向均匀布置两根连梁(见图 1),区别与带水平缝的双连梁,仅仅降低了连梁的刚度,这一做法可以使墙肢的受力更加均匀,避免局部的应力集中,有效增加了连梁的跨高比,改善连梁的延性,还可以解决连梁截面不足的设计难题。同时两根连梁之间的距离增大,施工难度不大。本文对在结构洞口设置双连梁的结构进行了抗震性能方面的全面研究。

2 计算模型

文中结构模型为 40 层框架核心筒结构中的纯核心筒部分,其中首层为 2 层高,高度为 12.6m 其余各 层均为 4.2m,总高度为172.2m,楼层标准平面图见图 2。模型中 X 方向有 3 片墙体,Y 方向有4 片墙体, 本算例模型中仅在 Y 方向的墙肢洞口处存在单双连梁区别,故以下各项指标均为Y方向。

墙肢和连梁的截面尺寸以及材料类别见表 1。核心筒内楼面梁为 C40 混凝土,截面为650mm×300mm。 双连梁与单连梁保持相同的面积配箍率(0.3%)和相同纵向钢筋配筋率(0.6%)。混凝土材料采用弹塑性损伤模型,可考虑材料拉压强度的差异,刚度的退化。PERFORM-3D 中混凝土的拉压是独立的,在本算例中未考虑混凝土的抗拉,假定受拉全部由钢筋承受。剪力墙约束边缘构件以及构造边缘构件采用约束区混凝土本构,非约束边缘构件的墙体使用普通混凝土本构。对于约束混凝土按照 mander 模型计算约束混凝土的本构。所有混凝土构件中的钢筋为 HRB400,钢筋采用双线型模型,在循环加载中无刚度退化。混凝土本构以及钢筋本构关系见图 3-4。由于双连梁结构中在层高的中间位置有一根连梁,所以沿层高方向将剪力墙沿高度方向细分为两个单元,作为对比在单连梁模型中,剪力墙单元也沿层高方向细分为两个单元。

本算例模型采用纤维截面来模拟剪力墙单元,墙体的非线性行为通过材料的非线性行为来模拟。连梁塑性铰基于弯矩-曲率关系的塑性铰定义,通过杆端塑性铰进行模拟,塑性变形集中于两端的塑性铰。计算分析模型中主要使用纤维单元模型和杆端弹簧模型,有效的降低了结构的自由度,在不失准确性的前提下, 提高了计算效率。

钢筋混凝土连梁采用的参数从 FEMA 356[5]的表格 6-18 中得到,该表是对应剪力墙之间的采用传统纵向钢筋的连梁的。

强度显著退化时的塑性铰 a = 0.025 rad,最大塑性转角 b = 0.05 rad,以及残余强度 c = 0.75。图 6 显示了连梁的弯矩与转角曲线。

对于跨高比小于 2.5 的单连梁,在大震下通常会出现剪切破环。对于模拟混凝土连梁时采用的参数,参照了FEMA 356 的表格 6-19,该表是对应的是采用传统纵向钢筋连梁的剪切塑性铰。这些参数包括:强度显著退化时的塑性铰 a = 0.012 rad,最大塑性转角 b= 0.025 rad,以及残余强度 c = 0.4。图 6 显示了连梁的剪切位移关系曲线。

由于两个连梁采用相同的纵向配筋率以及配箍率,故单连梁屈服弯矩比双连梁单根的弯矩屈服点有很 大的提高,剪切的屈服点也有了一倍以上的提高。

3 结构弹塑性能分析

按照基于性能的抗震设计方法,采用三维非线性分析与性能评估软件PERFORM-3D的纤维模型对上述结构进行弹塑性时程分析。从中国建研院 EQDB 数据库中选取三组地震波,计算时长为30s,加速度峰值 调幅为400gal(见图 8),按照 1:0.85 双向输入。形成六种工况。工况组合如表 2 所示:

两模型振型相同,在无双连梁方向结构的周期保持一致,模型中仅在一个方向存在差异性。

图 7-8 为两种连梁模型的楼层位移和层间位移角,通过对比发现双连梁比单连梁的楼层位移有所的增 加,双连梁在不增加材料的情况下,也能很好的控制了结构的位移。说明双连梁也能很好的维持结构的刚 度。双连梁对连梁跨高比的减小并没有带来结构刚度的显著降低。结构的位移反应和周期共同反应了双连 梁对结构刚度的影响较小。

结构的塑性发展

按照 FEMA356 确定了个构件相应的目标性能水准,IO、LS、CP 分别对应第一、第二、第三性能水准目标。

双连梁结构首先在 3-5 层的连梁达到第一性能水准(IO)随着地震动的不断增加,连梁的塑性损伤迅速增加,此时底部的少量剪力墙达到剪切 IO 水准,随后结构中下部连梁塑性损伤达到第二性能水准(LS),没有连梁进入塑性损伤第三水准(CP)。连梁的塑性铰沿层高方向均匀出现,在Y向中间两片墙体上,基本上所有的连梁均进入塑性,塑性铰的转动发展程度较大。连梁的抗剪都处于弹性,并且处于较低的需求能力 比水平(0.4 以下),剪力墙抗剪均维持在弹性状态。剪力墙中出现拉压屈服现象的数量不多,主要集中在底部一层和二层。结构的塑性损伤的出现与发展比较理想,双连梁有效的减缓了墙体的塑性铰的发展,结构的塑性损伤基本稳定。

单连梁结构,首先在 3-5 层的连梁达到第一性能水准(IO)随着地震动的不断增加,连梁的塑性损伤增加缓慢,此时底部的较多的剪力墙达到剪切 IO 水准,随着地震动的不断增加,仅有很少部分连梁进入塑性损伤第二水准(LS),多数连梁的塑性铰的转动处于较低的水平。各墙片中连梁的塑性铰仅出现在中下部,在楼层较高处的连梁没有进入塑性,仍处于弹性状态。连梁中剪力较大,在 Y 向中间两片内墙上,全部的连梁出现剪切铰,连梁的剪切承载能力不足,在Y向外侧两片墙体中,连梁的抗剪承载能力最高达到了0.6 的需求应力比。底部剪力墙抗剪的需求能力比在底层处于较高水平(0.6-0.7),底部部分剪力墙抗剪屈服,剪力墙拉压屈服区域较大,分布位置较高。随后结构的塑性损伤稳定。

结构的耗能性能见图 9,图为两模型在罕遇地震情况下的能量图,从图中可以看到结构总能量与各部分的耗能(势能、应变能、模态阻尼能、弹塑性变形能)的变化情况。单连梁模型中结构在 2-3s 左右进入塑性阶段,双连梁模型中结构在 1s 末进入塑性阶段,随后结构的塑性耗能随着地震的进行而不断增大,最后基本稳定。

双连梁模型在分析结束时结构弹塑性耗能占总能量的 50%-60%。单连梁模型在分析结束时弹塑性耗能占结构总能量的 40%-50%,说明单连梁耗散的地震能量较少,对比得出约有10%左右的地震能量在单连梁模型中由剪力墙来耗散。另外单连梁中墙体的拉压屈服的范围要大于双连梁,因此在单连梁模型中墙体参与耗能的比例高于双连梁模型。

4 结论

通过剪力墙双连梁与单连梁模型的弹塑性对比分析可以得出以下结论:

(1)剪力墙单连梁的抗剪承载能力不足,塑性铰在单连梁中发展能力较弱,多数连梁出现剪切破坏,而双连梁模型中,塑性铰发展良好,连梁截面具有足够的抗剪承载能力,塑性铰的塑性转动能力大,增加了结构的延性。

(2)双连梁模型中剪力墙塑性铰高度较低,剪力墙塑性损伤程度较低。单连梁模型中塑性铰发展的层数较高,剪力墙在底部塑性损伤集中,在连梁塑性铰出现后,剪力墙迅速屈服,连梁不能很好的发挥塑性耗 能能力。

(3)双连梁模型中剪力墙的应力分布均匀,在连梁与墙体的连接处对比于单连梁的相同位置,剪力墙中应力水平低。说明双连梁可以改善连梁与墙体连接处的应力分布,使应力分布更加均匀。

(4)结构的位移和自振周期比较接近,双连梁与单连梁相比,没有明显的降低结构的刚度。

(5)双连梁的塑性耗能占总能量的百分比高于单连梁,说明双连梁充分发挥了塑性耗能能力,有效保护了剪力墙结构,充分发挥了抗震设防第一道防线的作用。

采用双连梁的结构可以在控制跨高比小于 2.5均匀,很好地改善结构的延性,使剪力墙中应力分布更加均匀,墙体的塑性损伤明显降低,同时连梁中剪力明显降低,改善连梁超筋的情况。另外,该结构形式的连梁便于结构的施工,便于结构中管线的通过,具有良好的可操作性。

内容源于网络，如有侵权，请联系删除

相关资料推荐：

某剪力墙连梁节点构造及大样图设计

剪力墙连梁节点构造设计施工详图

知识点：剪力墙洞口双连梁设计研究