2021年度进展04：桥梁健康监测

1.引言本文将详细介绍桥梁健康监测的年度进展情况，文中的图表与数据主要来源于《Structural Health Monitoring》和《振动与冲击》等期刊杂志。进行桥梁健康监测时，每天会产生大量数据，因此，面对海量的监测数据，有必要采用合适的处理手段从中分析出有价值的信息，以为桥梁结构运营状态评估提供重要的科学参考依据。实时监测得到的信号数据的处理过程有如下几个关键点：

1.引言

本文将详细介绍桥梁健康监测的年度进展情况，文中的图表与数据主要来源于《Structural Health Monitoring》和《振动与冲击》等期刊杂志。进行桥梁健康监测时，每天会产生大量数据，因此，面对海量的监测数据，有必要采用合适的处理手段从中分析出有价值的信息，以为桥梁结构运营状态评估提供重要的科学参考依据。实时监测得到的信号数据的处理过程有如下几个关键点：

1）信号预警研究

目前，桥梁健康监测信号的预警方法主要分为固定阈值法和动态阈值法两种。固定阈值法是将修正后有限元模型的分析结果作为理论固定阈值；而动态阈值法则是依据海量监测信号的统计特性或回归模型，在信号趋势项基线上设定随之动态变化的阈值曲线。

2）自动化模态参数识别研究

在桥梁健康监测中，结构的模态参数识别通常颇具难度。桥梁结构的模态参数主要是指结构的频率、振型和阻尼比，它们反映了结构的系统特性。针对桥梁运营中的环境激励，研究者们已经提出多种较成熟的运营模态分析方法(OMA)，例如随机子空间法(SSI)、环境激励法(ERA)、频域分解法(FDD)、峰值拾取法(PP)、随机减量法(RDT)、时域参数识别法(ITD)等。上述OMA方法又可以分为频域方法(FDD、PP)和时域方法(SSI、ERA、RDT、ITD)。频域方法通常识别功率谱密度(PSD)的峰值或直接输出PSD矩阵的奇异值，但由于频域模态识别方法每次重新运算都需要初步校准，且对噪声非常敏感，因此该类方法在桥梁健康监测中存在较大局限性。时域方法通常着重于稳定图的自动解析，以获取有代表性的模态，目前大跨桥梁健康监测中使用最多的时域方法是随机子空间法(SSI)。然而，现阶段无论时域方法还是频域方法，都亟需解决如何高效过滤虚假模态这一难题，从而实现桥梁模态参数的自动化识别，为实时有限元模型修正和快速损伤诊断提供技术可能。

3）有限元模型修正研究

桥梁结构有限元模型修正通常是通过调整设计参数(密度和刚度)来实现的，调整参数的方法又分为灵敏度矩阵法(SA)和响应面法(RSM)，其中响应面法具有更高的计算效率。替代模型技术引入了参数敏感性分析的统计性质，将试验设计、参数子结构、多元逐步回归、假设检验等计入到结构有限元模型计算中，此外，替代模型技术还能与SA和RSM有机结合。近年来，为了提高复杂桥梁结构有限元模型修正的计算效率，越来越多的学者采用Kriging预估器和响应面模型等替代模型方法来逼近结构响应与修正参数之间的关系，以提升有限元模型修正的计算速率。

2.信号预警的研究进展

Yung-Bin等[1]采用Mask R-CNN深度学习方法，结合选定的局部冲刷公式和输沙方程，对冲刷深度演变的数学模型进行了模拟，进而提出了高墩桥梁的水位监测与信号预警方法；最后通过实验室和现场测量结果论证了所提方法的有效性。

曹晓龙[2]根据结构监测信号的特点，提出了基于监测数据时频域特征统计分析的桥梁多指标预警体系概念的初步设计，并将其预警等级依据指标阈值的设置划分为不同的层次，以实现针对不同程度损伤的预警目的，所建立的多级指标预警体系同时考虑了固定阈值法与动态阈值法两种解决方案。

霍明宇[3]引入动态时间规整(DTW)算法，对两条桥梁振动加速度响应时间序列进行相似性度量，计算两序列之间的DTW距离，并基于计算结果设定了损伤预警指标RDS，通过对南京大胜关长江大桥主跨加速度响应数据RDS指标与温度数据间的相关性进行分析，采用两级损伤指标建立了大跨桥梁振动信号的动态预警机制。

吴文广等[4]采用关联性趋势分析方法建立桥梁监测数据的关联性曲线作为信号动态预警的基准数学模型，再通过概率统计方法建立两线三区预警体系，最后以南京大胜关长江大桥运营监测系统作为工程实例进行验证(如图1所示)，结果表明：与结构响应数据固定且单一的时程预警指标相比，关联性趋势预警阈值随关联性特征变化而变化，具有更高的精度和灵敏度；这证明采用动态阈值法的综合预警体系能够更科学地实时预警，具有一般性和通用性。

图1 数据关联性曲线

赵大成等[5]以芜湖长江大桥健康监测系统为背景，首先分离环境温度及列车荷载作用下的挠度数据，然后分时段建立环境温度与对应非过车挠度的相关性模型并统计过车时段挠度变化幅值，最后基于相关性模型及统计分析结果为主梁挠度设定预警阈值。研究结果表明：主梁挠度主要由环境温度及列车荷载产生，环境温度与挠度存在显著线性相关关系，因此动态阈值法是更为科学的桥梁结构主梁挠度预警阈值设定方法。

Buckley等[6]使用动态谐波回归时间序列模型模拟应变响应变化趋势与温度激励之间的相关性关系，用来预测一座预应力混凝土桥梁的受力状态，从而对桥梁结构的早期损伤进行预警，取得了不错的效果。

Sarmadi等[7]依据极值、拟合优度理论以及无监督机器学习等方法，考虑了环境激励变化对结构响应趋势的影响，提出了桥梁结构动态预警阈值估计方法的概率统计方法，并通过Z24桥的实测模态特征数据验证了所提方法的可靠性。

3.自动化模态参数识别的研究进展

为了提升自动化OMA的运算效率，张秀林[8]提出了卷积神经网络(CNN)与快速搜索密度峰值聚类算法(FSDPC)相结合的模态参数自动识别方法，最后通过多座大跨桥梁的工程实例验证了所提方法不仅具有良好的计算效率，且精度也适用于结构模态参数的实时在线识别。梁鹏等[9]引入改进的模糊C均值聚类算法(FCM)和图切分算法自动确定最佳聚类数目，来达成稳定图自动识别；再通过建立数据解析过程，提出动态可变滑动数据窗，保证了自动识别的实时性；最后通过某拱桥模型验证了所提方法可行性。

为了减弱OMA中测试噪声和模型误差的影响,刘玲玲等[10]引入振型融合的不确定性量化分析，提出了模态参数识别的贝叶斯方法，最后通过一座斜拉桥的环境激励振动测试数据验证了所提方法的有效性，并探明了各测组数据质量及频带宽度等因素对整体振型不确定性的影响。

以往的OMA中往往仅将车辆荷载当作环境激励的一部分，而忽视了车辆本身具有的质量属性影响，因此贺文宇等[11]以SSI方法为例，研究运营模态分析中桥梁模态参数的变化情况，结果发现结构局部损伤和过桥移动车辆都会造成模态频率减小和振型改变，因此在实际模态测试中有必要考虑移动车辆作用并剔除其影响。

针对OMA中大跨柔性桥梁结构的相邻密集模态难以识别问题，Au等[12]分析了模态阶次的不确定性，提出了量化模态参数不确定性的解析表达式。与此同时，为避免SSI算法中虚假模态对模态参数识别的影响，王秋萍等[13]基于奇异熵增量的特性提出了一种系统阶次的计算方法，在稳定图中引入模态参数不确定度理论，构建模态参数的置信区间，形成带置信区间的稳定图，并通过对一座高速铁路连续梁桥的模态参数识别验证改进稳定图方法的有效性。针对SSI算法的系统定阶需人为参与、奇异值跳跃法难以确定高阶系统阶次的问题，陈永高等[14]采用“对数化处理”方式(如图2所示)，构建频率置信因子和振型置信因子来确定真实阶次的取值范围，再采用线性加权平均法构建置信系数，进而提出了确定结构系统真实阶次的新方法；最后将所提算法运用于某大型斜拉桥的模态参数识别，验证了所提方法的可靠性。

图2 结构系统阶次确定方法对比

同年，刘威等[15]采用敏感性分析方法研究了Toeplitz矩阵行块数和系统阶次在SSI-Cov算法中对模态识别结果的影响规律，研究结果表明：Toeplitz矩阵或系统矩阵的条件数越小，计算结果精度越高；识别频率、阻尼比的变异系数越小,对应的模态稳定图质量越好；通过奇异熵增量理论可准确识别结构的系统阶数，奇异熵增量的一阶灵敏度降至0时对应的阶数即为系统阶数的值。

4.有限元模型修正的研究进展

T.Svendsen等[16]利用实测的固有频率和模态保证准则(MAC)数据制定目标函数，采用灵敏度矩阵法对全尺寸钢桥进行模型修正，得到了可靠的桥梁结构基准模型。

大跨桥梁结构构造复杂，构件众多，导致有限元模型修正的计算效率低下。因此，2021年，学者们将目光聚焦到桥梁结构有限元模型修正的局部分析方案，力图抓住重点，“化简去繁”。宋晓东等[17]采用子结构方法化整体分析为局部分析，提升了大跨复杂桥梁结构有限元模型修正的计算效率，并以怒江特大桥工程实例得以验证。唐煜等[18]在保持梁单元模型计算效率优势的前提下，为尽可能提高桥梁结构有限元模型的精度，提出一种基于人工蜂群算法的桥梁结构有限元模型局部刚度修正方法，然后以某刚构体系斜拉桥塔梁连接处的有限元模拟为例，验证了采用所提方法修正后的宏观梁单元有限元模型的静动力学性能更加逼近实体模型。Salehi[19]为了提升桥梁健康监测中OMA的准确性，考虑了结构特性和边界约束在运营期内的变化，分析了桥梁结构模态参数对各种列车激励的敏感性以及边界条件的附加转动刚度，使用人工神经网络模型(ANN)修正某桥梁结构的有限元模型，取得了高精度的基准模型。

替代模型技术凭借其高效性和可靠性优点，依旧是年度热点。徐喆等[20]提出了一种基于麻雀搜索算法(SSA)和多项式响应面法的桥梁结构有限元模型修正方法，通过对高维局部损伤悬臂梁数值模型实施修正，验证了所提方法的可行性。秦世强等[21]为了更加合理地确定Kriging替代模型样本点数量，提高Kriging模型对目标函数极值区域的预测精度，提出了一种自适应Kriging模型并将其应用于桥梁结构有限元模型修正，最后以一座人行斜拉桥模型修正为例，建立了标准Kriging和自适应Kriging拟合的一阶频率响应面如图3所示，然后对比了自适应Kriging模型和标准Kriging模型的有限元模型修正结果，结果表明自适应Kriging模型能获得更好的修正结果。同年，秦世强[22]还将Kriging替代模型与改进的万有引力搜索算法(GSA)相结合，利用南中环桥荷载试验数据对初始有限元模型进行修正，得到了可靠的结构基准有限元模型。杨雅勋等[23]使用加权响应面法对以耿峪河大桥单梁有限元模型进行修正，采用中心复合试验设计法和方差分析筛选出显著性高的参数，从而建立了加权响应面替代模型，以测试荷载试验数据构造目标函数，结合混沌粒子群优化算法识别结构参数，所得结果良好。

图3 标准Kriging和自适应Kriging拟合的一阶频率响应面

Chen等[24]为了保证桥梁健康监测中结构状态预测(有限元模型修正)的及时性，分别采用响应面、支持向量回归和径向基神经网络(RBF)三种基于替代模型探索计算效率最高效的动态有限元模型修正方法，并且评估了中心复合设计抽样(CCD)和Box-Behnken设计抽样两种不抽样方法对模型修正结果的影响；经青马大桥工程的实例验证表明，替代模型类型对有限元模型修正结果的影响不显著，然而，抽样方法的选择对有限元模型修正结果的影响是非常显著的。

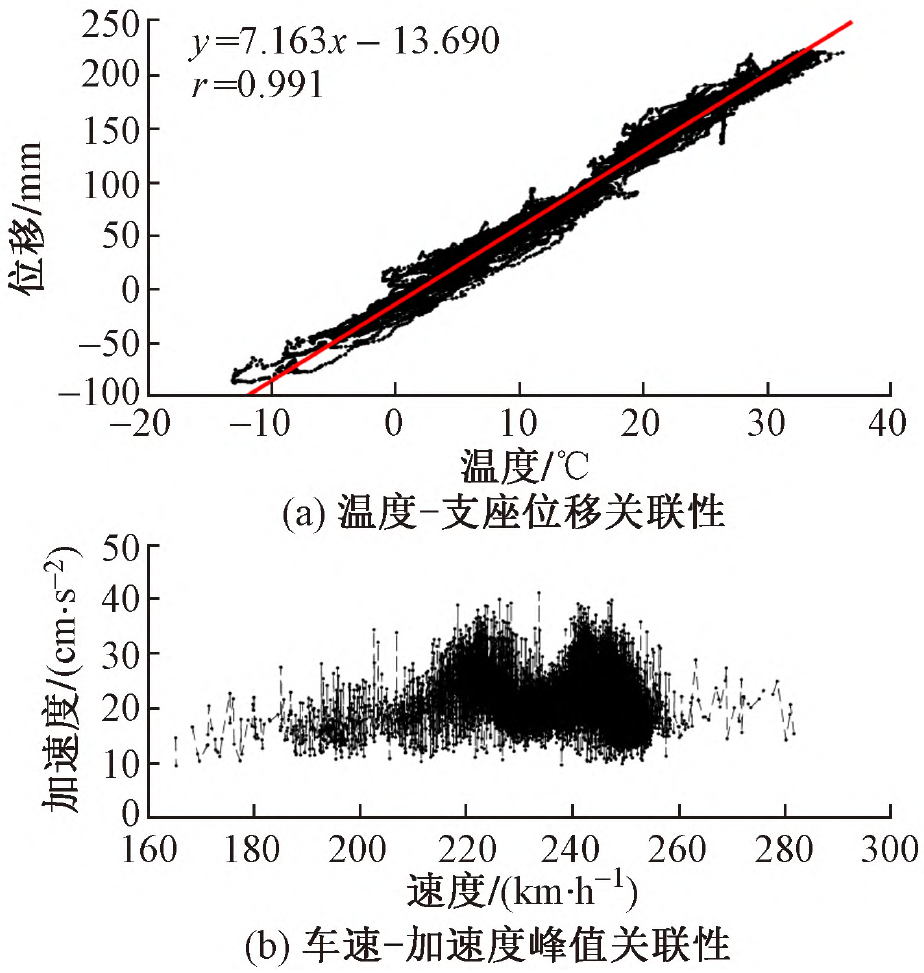
5.软件编制与实际工程应用

为从实测数据中获取更多的桥梁结构状态信息，基于.NET Framework 4.7平台和Windows 10操作系统，采用Microsoft Visual Studio 2019和Microsoft SQL Server 2019数据库作为系统开发工具，将西南交通大学智能桥梁团队前述研究成果积极推广应用于实际工程，在完成某悬索桥健康监测的过程中(见图4)，研发了以数据分析和处理为主要功能的桥梁健康监测软件系统。为快速有效地研发该系统，开发过程中采用了诸如Windows Presentation Foundation(WPF)技术、Model-View-View Model(MVVM)设计模式、Server Management Objects(SMO)技术、Code First等现代编程技术；同时结合桥梁养护维修规范，完成了某山区大跨高墩悬索桥健康监测数据处理分析系统的开发。系统界面截图如图5所示。

图4 某山区大跨悬索桥健康监测系统实施现场照片

图5 桥梁健康监测数据处理分析系统界面截图

6.展望

与上一年相比，2021年度桥梁结构模态参数的自动化识别研究除了仍旧尝试在提升运算效率、提高虚假模态辨识能力等方面取得进展外，还非常关注系统自适应定阶问题。有限元模型修正研究则在改进替代模型、优化识别方法层面上，开展了更深入的研究工作。桥梁损伤识别研究针对传统频域损伤指标(即模态参数)存在的问题，提出了基于桥梁健康监测系统信号异常变化的时域损伤指标。此外，在信号预警、有限元模型修正的相关研究进展中不难发现，数据融合方法作为新兴的桥梁健康监测方法策略，正受到越来越多的关注与应用。

作者介绍：

李乔，教授，博士生导师，国务院学位委员会学科评议组成员，全国土木工程专业评估委员会委员，在中国土木工程学会等多个学术组织中担任理事或常务理事。

邮箱：ql3721@vip.163.com

单德山 ，教授，博士生导师，西南交通大学智能桥梁团队学术带头人，主持多项国家重大科研项目，主持参与过多座大桥健康监测系统的设计实施和数据处理。

邮箱：dsshan@163.com

罗凌峰 ，博士生，师从单德山教授，参与了笋溪河大桥健康监测系统的设计实施和信号处理工作，研究方向是大跨桥梁位移信号分析与数据融合。

邮箱：526884687@qq.com

孙榕徽 ，博士生，师从单德山教授，西南交通大学智能桥梁团队成员，参与了笋溪河特大桥健康监测系统的信号分析工作，研究方向是桥梁健康监测与在役桥梁全寿命周期抗震性能。

邮箱：sunronghui0823@163.com

主要参考文献

[1] Lin Y B, Lee F Z, Chang K C, et al. The Artificial Intelligence of Things Sensing System of Real-Time Bridge Scour Monitoring for Early Warning during Floods[J]. Sensors, 2021, 21(14):4942.

[2] 曹晓龙. 基于监测数据时频域特征统计分析的桥梁安全预警研究[D]. 大连理工大学, 2021.

[3] 霍明宇. 基于时间序列相似性度量的铁路桥梁损伤识别研究[D]. 北京交通大学, 2021.

[4] 吴文广, 曹成斌, 刘兴旺,等. 基于移动区间关联性趋势的两线三区预警体系研究[J]. 铁道建筑, 2021, 61(12):71-75.

[5] 赵大成, 吴少雄, 刘兴旺,等. 芜湖长江大桥挠度预警阈值研究[J]. 铁道建筑, 2021, 61(3):24-27.

[6] Buckley T, Pakrashi V, Ghosh B. A dynamic harmonic regression approach for bridge structural health monitoring[J]. Structural Health Monitoring, 2021:147592172098173.

[7] Sarmadi H, Yuen K V. Early damage detection by an innovative unsupervised learning method based on kernel null space and peak-over-threshold[J]. Computer-Aided Civil and Infrastructure Engineering, 2021.

[8] 张秀林. 基于稳定图理论和机器学习的模态参数自动识别研究[D]. 哈尔滨工业大学, 2021.

[9] 梁鹏, 贺敏, 张阳,等. 实时在线桥梁模态参数自动识别[J]. 振动、测试与诊断, 2021, 41(1):76-84.

[10] 刘玲玲, 颜王吉, 李丹,等. 桥梁结构多测组振型融合的两阶段快速贝叶斯方法研究[J]. 噪声与振动控制, 2021, 41(4):182-189,197.

[11] 贺文宇, 丁绪聪, 任伟新. 环境激励下移动车辆对桥梁模态参数识别的影响研究[J]. 振动与冲击, 2021, 40(3):48-53.

[12] Siu-Kui A, James M.W.B, Binbin L, et al. Understanding and managing identification uncertainty of close modes in operational modal analysis[J]. Mechanical Systems and Signal Processing, 2021, 147.

[13] 王秋萍, 秦世强. 基于带置信区间稳定图的铁路连续梁桥模态参数识别[J]. 铁道建筑, 2021, 61(6):20-24.

[14] 陈永高, 钟振宇. 桥梁结构模态参数识别中系统阶次的自动辨识算法[J]. 振动工程学报, 2021, 34(4):680-689.

[15] 刘威, 杨娜, 白凡,等. 基于敏感性分析的协方差随机子空间方法参数优化[J]. 工程力学, 2021, 38(2):157-167,178.

[16] Svendsen B T, Petersen Y W, Frseth G T, et al. Improved finite element model updating of a full-scale steel bridge using sensitivity analysis[J]. 2021

[17] 宋晓东, 颜永逸, 李佳靖,等. 基于子结构的大型桥梁有限元模型修正方法[J]. 桥梁建设, 2021, 51(2):40-46.

[18] 唐煜, 岳杰, 华旭刚. 基于人工蜂群算法的桥梁有限元模型局部刚度修正[J]. 铁道科学与工程学报, 2021, 18(9):2333-2343.

[19] Mohammadreza S. Modal identification and finite element model updating of railway bridges considering boundary conditions using artificial neural networks[D]. Storby University, 2021.

[20] 徐喆, 辛景舟, 唐启智,等. 基于响应面法和麻雀搜索算法的结构有限元模型修正[J]. 科学技术与工程, 2021, 21(21):9094-9101.

[21] 秦世强, 廖思鹏, 黄春雷,等. 基于自适应Kriging模型的人行斜拉桥有限元模型修正[J]. 2021, 60(6):43-53.

[22] 秦世强, 甘耀威, 康俊涛. 基于改进万有引力搜索算法的南中环桥模型修正[J]. 振动与冲击, 2021, 40(19):116-124,136.

[23] 杨雅勋, 柴文浩, 杨福利,等. 基于加权响应面法和混沌粒子群优化算法的单梁有限元模型修正[J]. 兰州大学学报(自然科学版), 57(6):823-829.

[24] Xiao-Xiang C, Jian-Hua F, Zhi-Hong X. Finite element model updating for the Tsing Ma Bridge tower based on surrogate models[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2021.