位移法 首先将混凝土梁柱的节点“锁住”,此时混凝土梁两端为固定,弯矩图、变形图如下: 梁两端固定弯矩图 梁两端固定变形图 由于混凝土梁柱线刚度并不是无限大的,一旦把“锁”去掉,柱子就会协调梁的变形,梁端的变形释放一部分给柱子,梁的弯矩也会在此处释放给柱子一部分,弯矩图、变形图如下:
首先将混凝土梁柱的节点“锁住”,此时混凝土梁两端为固定,弯矩图、变形图如下:
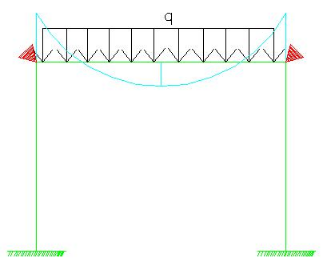
梁两端固定弯矩图

梁两端固定变形图
由于混凝土梁柱线刚度并不是无限大的,一旦把“锁”去掉,柱子就会协调梁的变形,梁端的变形释放一部分给柱子,梁的弯矩也会在此处释放给柱子一部分,弯矩图、变形图如下:

弯矩释放后弯矩图

变形释放后变形图
总结,力与变形之间是一一对应的关系,内力不好理解的时候,可以从变形的角度理解和分析。力与变形的弹性对应关系由胡克定律描述:材料受力之后,材料中的应力与应变(单位变形量)之间成线性关系,固体中的应力σ与应变ε成正比,即σ=Εε,式中E为常数,称为弹性模量。
多跨连续梁竖向荷载作用下的弯矩图如下:

实际案例:
梁截面 250×500,跨度为 6m,线荷载为 16KN/m,面荷载为 0(全房间开洞)。梁自重:0.25×0.5×25=3.125KN/m。
总线荷载 16+3.125=19.125KN/m;
 =(19.125×6×6)/12=57.375KN·m
=(19.125×6×6)/12=57.375KN·m
 =(19.125×6×6)/24=28.6875KN·m
=(19.125×6×6)/24=28.6875KN·m
 多跨连续梁弯矩图
多跨连续梁弯矩图
总结:
L 形节点位置:M 小(变形小);是由于在此位置梁端的 M(变形)释放给了柱子,
具体释放给柱子多少这主要取决于梁柱的刚度比;梁端M值小于 。
。
T 形节点位置:此处两端均有梁的变形和柱子的变形,三者的变形都在此处,梁两侧的变形“互顶”,柱子很难释放两侧梁的变形,所以此处的梁端弯矩会比 L 形节点位置弯矩大。
假设柱子的高度只有 300mm 高,此时柱的高度(L)很小很小,柱的线刚度 很大了,梁的变形很难释放给柱子。
很大了,梁的变形很难释放给柱子。

柱子无限短,刚度大(刚);则基本不会释放给柱子弯矩和变形,越接近纯固结;
柱子无限长,刚度小(柔);越容易协调梁的变形,接近简支,梁的 M 几乎全部释放给了柱子。
所以说柱子的高度对梁的弯矩影响很大,实际工程中,当建筑层高调整时,要将梁柱配筋进行核对校验,特别要注意边跨的配筋。
实际案例:
此模型仅对柱高进行调整,参数信息,地震分组等均未调整。柱高 3m,恒荷载作用下的弯矩图:

柱高 3 米弯矩图
柱高 5m,恒荷载作用下的弯矩图:

柱高 5 米弯矩图
本文来源于网络,如涉及侵权,请联系删除!
