知识点:压控电压源二阶低通滤波器 正文: 第一步:根据物理模型推导出传递函数,根据传递函数的波特图评估滤波器性能 二阶有源低通滤波器有几个特性。截止频率点代表该频率处的幅值下降到-3db(对应的时域增益为1/sqrt(2)),也是低通滤波器的带宽,该频率点相位滞后90度。10倍截止频率处,幅值下降到-40db;100倍截止频率处,幅值下降到-80db,以-40db/十倍频程速率下降,比一阶低通滤波器对高频信号衰减的更快。从波特图看出,频率信号经过滤波器后,相位产生了延迟,频率越大相位延迟越大,频率无穷大时相位延迟趋近180度,对应时域增益为0。
知识点:压控电压源二阶低通滤波器
正文:
第一步:根据物理模型推导出传递函数,根据传递函数的波特图评估滤波器性能
二阶有源低通滤波器有几个特性。截止频率点代表该频率处的幅值下降到-3db(对应的时域增益为1/sqrt(2)),也是低通滤波器的带宽,该频率点相位滞后90度。10倍截止频率处,幅值下降到-40db;100倍截止频率处,幅值下降到-80db,以-40db/十倍频程速率下降,比一阶低通滤波器对高频信号衰减的更快。从波特图看出,频率信号经过滤波器后,相位产生了延迟,频率越大相位延迟越大,频率无穷大时相位延迟趋近180度,对应时域增益为0。
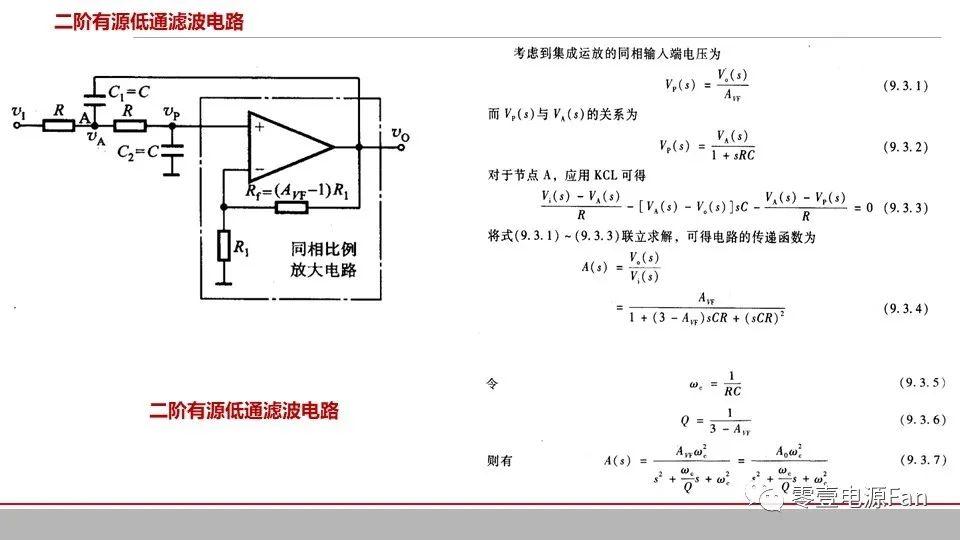


品质因数Q也是设计二阶低通滤波器的关键参数。当Q大于1时,截止频率附近的信号会被放大,跟需要滤除干扰信号是相违背的,所以实际低通滤波器设计中Q通常都是小于1。而当Q为较小的正值时,对低频信号相位影响又比较大,当Q小于0时,滤波电路又是不稳定的,实际工程中一般折中选择Q=0.707。
第二步:已知典型滤波器的传递函数去设计数字滤波器。
根据干扰信号幅值和频率,本着有用信号的幅值和相位不受滤波器影响,干扰信号被衰减掉,合理的选择滤波器类型和滤波器参数。
以二阶低通滤波器为例,设定典型二阶低通滤波器的品质因数Q,采样周期Ts,以及滤波截止频率fc,分析其频率响应,是否达到设计要求。然后通过离散方法,得到离散域传递函数,再得到差分方程,有了差分方程,就可以写出滤波器函数。



第三步:仿真验证。


相关推荐链接:
