1.竖向荷载作用下的受力原理竖向荷载包括恒荷载、活荷载。1.1位移法首先对混凝土梁柱的节点“锁住”,此时混凝土梁两端为固定,弯矩图、变形图如下:图2-1 梁两端固定弯矩图图2-2 梁两端固定变形图由于混凝土梁柱线刚度并不是无限大的,一旦把“锁”去掉,柱子就会协调梁的变形,梁端的变形释放一部分给柱子,梁的弯矩也会在此处释放给柱子一部分,弯矩图、变形图如下:2-3弯矩释放后弯矩图
1.竖向荷载作用下的受力原理
竖向荷载包括恒荷载、活荷载。
1.1位移法
首先对混凝土梁柱的节点“锁住”,此时混凝土梁两端为固定,弯矩图、变形图如下:
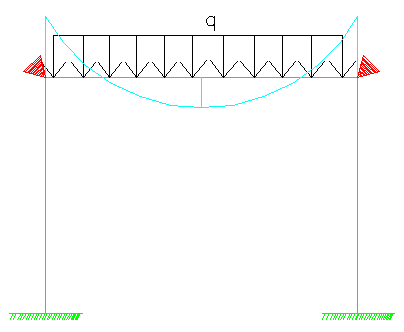
图2-1 梁两端固定弯矩图

图2-2 梁两端固定变形图
由于混凝土梁柱线刚度并不是无限大的,一旦把“锁”去掉,柱子就会协调梁的变形,梁端的变形释放一部分给柱子,梁的弯矩也会在此处释放给柱子一部分,弯矩图、变形图如下:

2-3弯矩释放后弯矩图

2-4 变形释放后变形图
总结,力与变形之间是一一对应的关系,内力不好理解的时候,可以从变形的角度理解和分析。
1.2多跨连续梁的受力
(1)多跨连续梁竖向荷载作用下的弯矩图如下:

2-5 多跨连续梁弯矩图
(2)实际案例:
梁截面250×500,跨度为6m,线荷载为16KN/m,面荷载为0(全房间开洞)。
梁自重:0.25×0.5×25=3.125KN/m
总线荷载16 3.125=19.125KN/m
M支=(19.125×6×6)/12=57.375KN·m
M中=(19.125×6×6)/24=28.6875KN·m

2-6 多跨连续梁弯矩图
总结:
L形节点位置:M小(变形小);是由于在此位置梁端的M(变形)释放给了柱子,具体释放给柱子多少这主要取决于梁柱的刚度比;梁端M值小于1/12ql2。
T形节点位置:此处两端均有梁的变形和柱子的变形,三者的变形都在此处,梁两侧的变形“互顶”,柱子很难释放两侧梁的变形,所以此处的梁端弯矩会比L形节点位置弯矩大。
1.3极限思维了解变形协调
假设柱子的高度只有300mm高,此时柱的高度(L)很小很小, 柱的线刚度( )很大了,梁的变形很难释放给柱子。
)很大了,梁的变形很难释放给柱子。

柱子无限短,刚度大(刚);则基本不会释放给柱子弯矩和变形,越接近纯固结;
柱子无限长,刚度小(柔);越容易协调梁的变形,接近简支,梁的M几乎全部释放给了柱子。
所以说柱子的高度对梁的弯矩影响很大,假如出图后,建筑的层高变了,一定要校对一遍梁柱的配筋。
1.4案例
此模型仅对柱高进行调整,参数信息,地震分组等均未调整。
(1)柱高3m,恒荷载作用下的弯矩图:

柱高3米弯矩图
(2)柱高5m,恒荷载作用下的弯矩图:

柱高5米弯矩图
2.水平荷载作用下的受力分析
水平荷载包括地震作用,风荷载。
2.1反弯点
反弯点:弯矩一正一负的零点位置。
反弯点的形成是因为梁柱线刚度比不是无限大,从变形来讲是因为柱子上下有转角,从而出现反弯点。

2.2水平荷载作用下的弯矩及变形

水平作用下的弯矩图
在水平力F的作用下,柱的底部外侧受拉,顶部的内侧受拉;梁的左端底部受拉,右侧梁顶受拉。(粗线表示受拉侧)。
2.3框架结构变形图

框架结构的变形图在柱底柱顶垂直于刚节点,框架结构的变形为剪切型变形,决定了框架结构的位移底部最大,从而影响了框架结构的很多性能(如:不能做很高、填充墙在地震时候是底层破坏严重等)。
思考:
(1)框架结构与剪力墙结构变形图对比、分析。
(2)分析次梁在水平力作用下的弯矩图。
