知识点：微分运算电路

很多朋友觉得PID是遥不可及，很神秘，很高大上的一种控制，对其控制原理也很模糊，只知晓概念性的层面，知其然不知其所以然，那么本文从另类视角来探究微分、积分电路的本质，意在帮助理解PID的控制原理。

（PID：P表示比例控制；I表示积分控制；D表示微分控制）

在认清微分、积分电路之前，我们都知道电容的特性：电容的电流超前电压相位90°，很多教材都这么描述，让人很费解，其本质又是什么呢？

电容的本质

要彻底掌握微分、积分电路或PID控制思路，首先得了解电容。

电容就是装载电荷的容器，从微观角度看，当电荷流入容器时，随着时间的变化极间电场逐渐增大。

以图1为例：

• 充电开始时Uc=0V，压差△U=Ur=Ui，此刻容器内无电荷，也就无电场排斥流入的电荷；所以电流Ic最大，表现为容抗最小，近似短路；
• 当Uc上升，压差△U开始减小，该过程形成电场，容器开始排斥流入的电荷；电流Ic逐渐减小，表现为容抗逐渐增大；
• 当Uc=Ui，压差△U=Ur=0V，此刻容器内电场最强，以最大排斥力阻止流入的电荷；电流Ic=0，表现为容抗最大，近似开路。
  

图1 电容容器充电模型

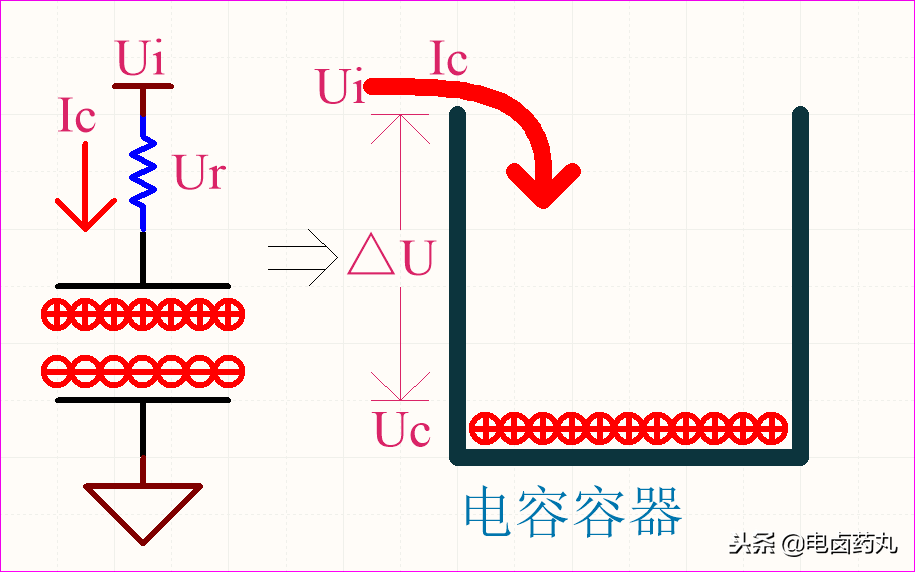
当电荷流出容器时，随着时间的变化极间电场逐渐减小；该放电过程的电容可看成是一个内阻为0的电压源，以图2为例（移除电源并接地）：

• 放电开始时Uc=Ui，此刻容器内充满电荷，因此电场最强，而电阻不变，则放电电流Ic最大（方向与充电相反），电阻两端的电压Ur=Uc，则Ur=Ui；
• 当Uc下降，该过程电场减弱，放电电流Ic逐渐减小，Ur=Uc也逐渐减小；
• 放电耗尽Uc=0V，此刻容器内无电荷，因此无电场，Ur=0V。
  

图2 电容容器放电模型

电容就好比水桶一样，流入的水流无论是大还是小，水位的变化一定是从最低位开始连续上升的；而电容内的电荷也是逐渐从0开始积累起来的，积累过程与自然常数e有关系，这里就不深入讨论了。

图3就是电容充放电的电压-电流曲线。

图3 电容充放电，电压-电流曲线

联系前面的分析，可总结为：

• 电容电压不能突变，电流可突变（教材的定义是电容的电流与电压的变化率成正比）；
• 充电过程中的电容可等效成一个可变电阻，放电过程中的电容可等效成一个电压源；
• 电容电流反映的是单位时间内流动的电荷量，电容电压（或电场）反映的是电荷量的多少。通俗的理解就是流动的电荷才会导致电荷量多少的变化（与①相吻合）；用数学语言描述则是电容的电流超前电压相位90°；
• 电容充放电速度与电容和电阻大小有关。

微分电路和积分电路

对电容充分了解之后，首先我们先来认识最简单的分压电路，如图4根据欧姆定律VCC=2.5V，该纯阻性的分压电路就是比例运算电路的雏形。

图4 分压电路

如图5，我们把R2换成104（0.1μF）电容，C1电容充满电后近似开路，VCC=5V；该电路就是积分运算电路的雏形。那么把5V改成信号源就构成了低通滤波电路。

图5 积分电路

如图6为上图的充电波形，红色表示5V的波形，蓝色表示VCC的波形，因为电容充电时的容抗由小变大直至开路，所以分压VCC也由小变大直至为5V。而且电容充电需要一定的时间，导致VCC的波形要缓一些。（该5V是开关电源上电软启动时的输出波形）

图6 积分电路波形

把图4图5组合就得到图7的电路，这就是我们经常使用的PI电路（比例积分），在参考电压或分压电路里很常见，加电容的目的就是增加延时性，稳定VCC的电压不受5V波动而波动，VCC=2.5V。

图7 PI电路

把图5中电容和电阻的位置交换一下得到如图8的电路，C1电容充满电后近似开路，VCC=0V；该电路就是微分运算电路的雏形。那么把5V改成信号源就构成了高通滤波电路。

图8 微分电路

如图9为上图的充电波形，红色表示5V的波形，蓝色表示VCC的波形，因为电容充电时的容抗由小变大直至开路，所以分压VCC由大变小直至为0V。也就是红色波形从0开始跳变一瞬间，VCC已经是最大值，所以微分有超前预判的性质（反映的是输入信号的变化率）。

图9 微分电路波形

如图10为（反相）比例运算电路。

图10 比例运算电路

如图11，Uo与Ui成线性关系。

图11 比例运算电路波形

如图12、图13为微分运算电路的充放电过程：

充电过程的电容C1可等效成一个可变电阻，C1开始充电时的容抗为0，电压不可突变则电压为0，运放-输入端得到的分压为正最大峰值，于是Uo为运放的负最大峰值，随着电容充满电，U0逐渐变为0。

图12 微分运算电路-充电

放电过程的电容C1可等效成一个电压源，且电压不可突变，此时电流反向为最大值，R1电压瞬间反向也为最大值，运放-输入端得到的分压则为负最大峰值，于是Uo为运放的正最大峰值，随着电容放完电，U0逐渐变为0。

图13 微分运算电路-放电

如图14为微分运算电路的输入输出波形，联系前面的分析结果，则Uo反映的是Ui的变化率，这样就达到了预判超前的效果。

图14 微分运算电路波形

如图15为微分运算仿真电路，为了防止运放出现饱和，必须限制输入电流，实际使用时需要在电容C1输入端串联一个小电阻R2。串联电阻后的电路已经不是理想微分运算电路了，但是只要输入信号周期大于2倍RC常数，可以近似为微分运算电路。

图15 微分运算仿真电路

如图16为微分运算仿真电路波形，其中IN-为运放-输入端的波形。

图16 微分运算仿真电路波形

如图17、图18为积分运算电路的充放电过程：

充电过程的电容C1可等效成一个可变电阻，C1开始充电时的容抗为0，电压不可突变则电压为0，运放-输入端得到的分压为0，于是Uo为0，随着电容充满电，运放-输入端得到的分压为正最大值，U0为运放的负最大峰值。

图15 积分运算电路-充电

放电过程的电容C1可等效成一个电压源，且电压不可突变，运放-输入端得到的分压也不可突变，随着电容放完电，于是Uo由负最大峰值逐渐变为0。

图16 积分运算电路-放电

如图17为积分运算电路的输入输出波形，联系前面的分析结果，则Uo反映的是Ui的积累过程，这样就达到了延迟稳定的效果。

图17 积分运算电路波形

如图18为积分运算仿真电路，为了防止运放出现饱和，实际使用时需要在电容C2两端并联一个电阻R3。并联电阻后的电路已经不是理想积分运算电路了，但是只要输入信号周期大于2倍RC常数，可以近似为积分运算电路。

图18 积分运算仿真电路

如图19为积分运算仿真电路波形，其中IN-为运放-输入端的波形。

图19 积分运算仿真电路波形

要点：

• 微分、积分运算电路利用了电容充放电时其电压不可突变的特性达到调节输出的目的，对变化的输入信号有意义；
• 微分D控制有超前预判的特性，积分I控制有延迟稳定的特性，在PID调节速度上，微分D控制＞比例P控制＞积分I控制。

相关推荐链接：

1、某地综合楼电路设计施工图（共5张）

2、共享资料 电力线路变压器等值电路