摘 要 1994年美国北岭地震、1995年日本阪神地震的灾害调查发现传统抗弯钢框架结构的梁柱连接节点出现了大量的脆性破坏,导致具有良好延性行为的抗弯钢框架结构变形能力未能得到充分发挥,结构整体抗震性能较差。因此,梁柱连接节点性能的优劣成为决定抗弯钢框架结构抗震性能好坏的关键因素。为适应公共建筑跨度大的特点,国内外一些大型公共建筑(如医院、商场、体育场馆等)逐渐采用特殊桁架式钢框架结构(简称STMF)。STMF结构具有抗侧刚度大、水平承载力高、耗能性能优良等优点,具有广阔的应用前景。但钢桁架与钢柱之间的连接节点易于断裂,特别是腹杆、弦杆与钢柱的连接焊缝处极易脆断,导致STMF结构的延性及变形能力较差。目前,国内外学者对STMF连接节点的研究仍相对较少,不利于STMF 结构的工程推广应用。为明晰STMF连接节点的滞回性能,以STMF结构的边柱节点作为研究对象,通过有限元方法分析了STMF连接节点的受力特征,明晰了相关设计参数对其滞回性能的影响,为其工程应用提供参考。
摘 要
1994年美国北岭地震、1995年日本阪神地震的灾害调查发现传统抗弯钢框架结构的梁柱连接节点出现了大量的脆性破坏,导致具有良好延性行为的抗弯钢框架结构变形能力未能得到充分发挥,结构整体抗震性能较差。因此,梁柱连接节点性能的优劣成为决定抗弯钢框架结构抗震性能好坏的关键因素。为适应公共建筑跨度大的特点,国内外一些大型公共建筑(如医院、商场、体育场馆等)逐渐采用特殊桁架式钢框架结构(简称STMF)。STMF结构具有抗侧刚度大、水平承载力高、耗能性能优良等优点,具有广阔的应用前景。但钢桁架与钢柱之间的连接节点易于断裂,特别是腹杆、弦杆与钢柱的连接焊缝处极易脆断,导致STMF结构的延性及变形能力较差。目前,国内外学者对STMF连接节点的研究仍相对较少,不利于STMF 结构的工程推广应用。为明晰STMF连接节点的滞回性能,以STMF结构的边柱节点作为研究对象,通过有限元方法分析了STMF连接节点的受力特征,明晰了相关设计参数对其滞回性能的影响,为其工程应用提供参考。
首先,设计了STMF连接节点的BASE试件,利用 CAD程序建立其三维几何模型,使用Hypermesh程序对其进行了网格划分,采用ABAQUS程序建立了微观有限元模型并进行了滞回性能分析。其次,在BASE试件的基础上,衍生设计了3个系列STMF连接节点,重点考察了弦杆截面、桁架高度、端斜腹杆截面等主要因素对其滞回性能、抗弯承载力、变形能力、屈服模式、应力分布的影响。
分析发现:STMF连接节点中桁架下弦杆的Mises应力水平相对较高,端节间的下弦杆在弹塑性阶段易出现整体失稳,加载后期还会出现局部失稳;随着弦杆截面的增加,STMF连接节点的抗弯承载力、初始转动刚度、耗能能力均呈增大趋势,但对STMF连接节点滞回曲线的形状影响较小;随着桁架高度的增加,STMF连接节点的抗弯承载力、初始转动刚度均呈显著增加趋势,其耗能能力略呈增大趋势但破坏模式并未显著改变;在桁架端部斜腹杆未屈曲的前提下,改变端斜腹杆截面对STMF连接节点的滞回性能、抗弯承载力、节点转动刚度、耗能能力影响不明显,其受力模式和应力分布并未发生显著改变。
0 引 言
特殊桁架式钢框架(简称STMF)是通过采用钢桁架替代传统实腹式框架梁所形成的一种抗侧力结构,适用于大跨度公共建筑,如医院、商场、体育场馆等,具有抗侧刚度大、水平承载力高等特点。
20世纪90年代美国学者Goel 教授较早地开展了特殊桁架式钢框架结构的滞回性能研究,发现桁架中斜腹杆受压屈曲导致结构呈脆性破坏模式。为避免或减缓桁架中腹杆屈曲问题,一些学者提出在桁架中部设置空腹节间的改良措施,用于提高STMF结构的变形能力。通过在空腹节间设置耗能支撑实现了提高变形及耗能能力的双重功能。此外, 部分学者对STMF结构的设计方法、损伤评估、倒塌性能进行了大量研究。但是,目前对特殊桁架式钢框架连接节点的相关研究偏少,特别是针对钢桁架与钢柱连接节点的滞回性能仍缺乏系统研究。基于此,本文采用ABAQUS程序分析了弦杆截面、桁架高度、端斜腹杆截面等因素对STMF连接节点滞回性能的影响,为其工程应用提供参考。
1 有限元模型的建立
1.1 BASE试件设计
为研究STMF连接节点的滞回性能,设计了1个BASE试件,几何尺寸见图1。钢柱高度为 4700 mm,桁架长度为 5200 mm, 桁架高度为800 mm。钢柱采用 H550×550×16×24,桁架端部斜腹杆采用 H200×150×6×10,其余腹杆采用 H150×100×6×8,弦杆采用 H200×150×6×10。BASE试件的所有构件均选用Q345B级钢材。
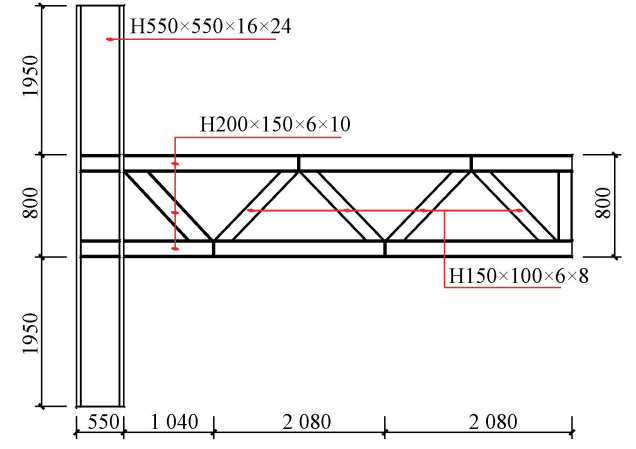
图 1 BASE 试件的几何尺寸
1.2 有限元模型
考虑到STMF连接节点建模的复杂性,本文利用CAD程序建立其三维几何模型,使用Hypermesh程序对其进行了网格划分,采用ABAQUS程序建立了BASE试件的精细化有限元模型,见图2。其中,周边钢柱、钢梁、腹杆、弦杆均采用SR4壳单元。通过对桁架梁上表面所有节点的面外 z 方向施加位移约束,用于反映楼板的约束效应。通过对柱顶和柱底表面所有节点进行耦合来处理反映节点的边界约束,即对柱底耦合点沿 x 、 y 、 z 方向施加位移约束,对柱顶耦合点沿 x 、 z 方向施加位移约束,用于模拟钢柱两端的铰接方式。通过对桁架端部竖腹杆施加耦合,并沿 y 方向施加竖向位移。

图 2 BASE 试件的有限元模型
有限元模型中钢材弹性模量 E = 2.06 ×10 5 MPa,屈服强度 f y = 345 MPa,泊松比 ν = 0.3,强化阶段的切线模量取 0.02 E ,采用双线性随动强化模型,利用Mises屈服准则考虑钢材的包辛格效应。
1.3 加载制度
BASE试件采用相关文献建议的加载制度,见图3。全程采用位移控制加载,每级荷载循环2次。其中, θ 为节点转角, N 为循环数。

图 3 加载制度
2 弦杆截面对STMF连接节点力学性能影响
为研究弦杆截面对STMF连接节点滞回性能的影响,设计了CSS系列试件。其中,CSS-1试件的弦杆采用 H200×200×6×10,CSS-2试件的弦杆采用H200×100×6×10,其他参数与BASE试件相同。
2.1 CSS系列试件的Mises应力分布
图4给出了CSS系列试件在节点转角 0.02 rad时的Mises应力分布。可知,尽管桁架弦杆截面不同,但桁架受力特征相似,与钢柱连接处的下弦杆先屈曲后屈服,其他节间弦杆及腹杆应力水平相对较低。通过提取加载至节点转角 0.02 rad 时CSS系列试件下弦杆的面外变形发现:CSS-1试件的下弦杆面外变形为 15.89 mm,略小于BASE试件对应弦杆的面外变形(16.78 mm);CSS-2试件的下弦杆面外变形为 19.46 mm。即增加弦杆截面可减小Mises应力,降低桁架下弦杆的面外变形。

a—BASE; b—CSS-1; c—CSS-2。
图 4 节点转角 0.02 rad 时CSS系列试件的Mises应力分布 MPa
2.2 CSS系列试件的滞回曲线
图5给出了CSS系列试件的滞回曲线。可知,由于桁架梁具有非对称的几何特征,导致所获得的滞回曲线呈明显的非对称分布。特别是加载至后期的弹塑性阶段,由于桁架梁下弦杆端部节间自由长度较大,致使受压时出现轻微整体失稳,弦杆板件出现局部失稳现象,节点的负向抗弯承载力略低,滞回曲线出现轻微捏缩特征。随着桁架弦杆截面的增加,滞回环略呈增大趋势,滞回曲线形状并未发生本质改变。

图 5 CSS系列试件的滞回曲线
2.3 CSS系列试件的骨架曲线
图6给出了CSS系列试件的骨架曲线。可知, CSS系列试件的骨架曲线具有显著的双线性特征,试件均进入弹塑性状态。BASE试件的正、负向抗弯承载力为 +1459.1、-1436.1 kN·m, 分别 比CSS-1试件的抗弯承载力低 25.3%、22.1%, 比CSS-2试件高 28.9%、17.9%。表明随着桁架弦杆截面的增加, CSS系列试件的抗弯承载力呈增大趋势。

图 6 CSS系列试件的骨架曲线
2.4 CSS系列试件的节点转动刚度
转动刚度的退化规律可间接反映节点在加载过程中的损伤历程。图7给出了CSS系列试件的节点转动刚度退化曲线,其中, K 为CSS系列试件的节点转动刚度。可知:BASE试件平均初始转动刚度为147.2 MN·m/rad,CSS-1试件平均初始转动刚度为166. 6 MN·m/rad,CSS-2试件的平均初始转动刚度为 128.5 MN·m/rad。即增加弦杆截面可显著提高STMF连接节点的初始转动刚度。在节点转角小于0.01 rad 时,CSS系列试件基本处于弹性阶段。随着节点转角的增加,CSS系列试件逐渐进入弹塑性阶段,节点转动刚度逐渐降低,但退化均匀、缓慢。

图 7 CSS系列试件的节点转动刚度退化曲线
2.5 CSS系列试件的滞回耗能
耗能能力是评价结构或构件抗震性能的重要指标,一般可采用无量纲的等效黏滞阻尼比( ζ eq )描述。等效黏滞阻尼比可反映出结构或构件滞回曲线的捏缩程度(图8) ,按式(1)计算。

图9给出了CSS系列试件的等效黏滞阻尼比。可知:由于增加弦杆截面,即弦杆翼缘宽度增加,导致其翼缘宽厚比增大,致使弦杆发生局部屈曲,导致STMF连接节点的滞回曲线趋于捏缩,耗能能力降低;CSS-1试件弦杆的翼缘宽厚比为9.7,其最大等效黏滞阻尼比为0.28;BASE试件弦杆的翼缘宽厚比为7.2,其最大等效黏滞阻尼比为0.30;CSS-2试件弦杆的翼缘宽厚比为4.7,其最大等效黏滞阻尼比为0.36。总体上,随着桁架弦杆翼缘宽厚比的降低,CSS系列试件的耗能能力呈增大趋势。

图 8 等效黏滞阻尼比的计算示意

图 9 CSS 系列试件的等效黏滞阻尼比
3 桁架高度对STMF连接节点力学性能影响
为研究桁架高度对STMF连接节点滞回性能的影响规律,设计了TH系列试件。其中,TH-1试件的桁架高度为 600 mm, TH-2试件的桁架高度为1000 mm,其他参数与BASE试件相同。
3.1 TH系列试件的Mises应力分布
图10给出了TH系列试件在节点转角 0.02 rad 时的Mises应力云图。可知:尽管桁架高度不同,桁架受压屈曲模式相似,均为与钢柱连接处下弦杆先屈曲;加载至节点转角 0.02 rad 时, TH-1试件的Mises应力的最大值为 373.6 MPa,略低于BASE试件,TH-2试件的Mises应力的最大值为 457.6 MPa,高于BASE试件。此外,通过提取当前荷载级别下TH系列试件端部下弦杆面外屈曲变形发现:TH-1试件的下弦杆面外屈曲变形为 10.69 mm,比BASE试件低36.3%;TH-2试件的下弦杆面外屈曲变形为 19.47 mm,比BASE试件高16%。总体上,随着桁架高度的增加,TH系列试件的节点端部区域的应力及面外屈曲变形呈增大趋势。

a—TH-1; b—TH-2。
图 10 节点转角 0.02 rad 时TH系列试件的Mises应力分布 MPa
3.2 TH系列试件的滞回曲线
图11给出了TH 列试件的滞回曲线。可知,TH系列试件的滞回曲线仍呈明显的非对称特征,改变桁架高度对TH系列试件的抗弯承载力影响较大,但对滞回曲线形状影响较小。

图 11 TH系列试件的滞回曲线
3.3 TH系列试件的骨架曲线
图12 给出了TH系列试件的骨架曲线。可知,TH-1试件的正、负向峰值抗弯承载力分别为1183, -1225.7 kN·m, 分别比BASE试件低12.3%、20%。TH-2试件的正、负向峰值抗弯承载力分别为1781.7,-1834.4 kN·m,比BASE试件分别高 22.1%、27.7%。总体上,随着桁架高度的增加,TH系列试件的节点抗弯承载力呈增大趋势。

图 12 TH系列试件的骨架曲线
3.4 TH系列试件的节点转动刚度
图13给出了TH系列试件的节点转动刚度退化曲线。可知:TH系列试件的正、负向抗侧刚度退化曲线基本对称;在节点转角小于 0.01 rad 时,TH系列试件处于弹性阶段,其中,TH-1试件的平均初始转动刚度为 106.6 MN·m/rad,比BASE试件低27.6%; TH-2试件的平均初始转动刚度为194.6 MN·m/rad,比BASE试件高 32%。在节点转角超过 0.01 rad 后,TH系列试件的节点转动刚度退化均匀,未出现脆性破坏。

图 13 TH系列试件的节点转动刚度
3.5 TH系列试件的耗能能力
图14给出了TH系列试件的等效黏滞阻尼比。可知,TH-1试件在进入弹塑性阶段的最大等效黏滞阻尼比为0.295,与BASE试件结果相近,略低于TH-2试件的最大等效黏滞阻尼比(0.321)。这说明改变桁架高度对STMF连接节点的滞回曲线形状产生一定影响,随着桁架高度的增加,其耗能能力略呈增大趋势。

图 14 TH系列试件的等效黏滞阻尼比
4 端斜腹杆对STMF连接节点力学性能影响
为研究端斜腹杆对STMF连接节点滞回性能的影响规律,设计了SIWM系列试件。其中,SIWM-1试件端斜腹杆截面为 H200×100×6×10,SIWM-2试件端斜腹杆截面为 H150×100×6×8,其他参数与BASE试件相同。
4.1 SIWM系列试件的Mises应力分布
图15给出了SIWM系列试件在节点转角0.02 rad 时的Mises应力云图。可知:尽管桁架端斜腹杆截面不同,但桁架弦杆受压屈曲模式相似,仍为与钢柱连接处下弦杆的端部节间先屈曲。通过提取加载至节点转角 0. 02 rad 时的Mises应力及下弦杆面外屈曲变形发现:SIWM系列试件的最大Mises应力为 393.6~418.3 MPa,桁架下弦杆面外屈曲变形为 16.78~18.69 mm。总体上,在桁架端斜腹杆未发生显著屈曲的前提下,因弦杆截面未发生改变,仅改变端部斜腹杆截面对桁架弦杆的Mises应力及面外变形影响较小。

a—SIWM-1; b—SIWM-2。
图 15 节点转角 0.02 rad 时SIWM系列试件Mises应力分布 MPa
4.2 SIWM系列试件的滞回曲线
图16给出了SIWM系列试件的滞回曲线。可知,SIWM试件的滞回曲线与BASE试件的滞回曲线几乎重合,充分说明,当SIWM节点的破坏模式未发生变化时,改变桁架端斜杆截面对STMF连接节点的滞回曲线形状的影响可忽略。

图 16 SIWM系列试件的滞回曲线
4.3 SIWM系列试件的骨架曲线
图17给出了SIWM系列试件的骨架曲线。可知:SIWM-1试件正、负向的峰值抗弯承载力分别为1463.4,-1413.9 kN·m,与BASE试件的抗弯承载力基本相等。当端部斜腹杆采用 H150×100×6×8 截面时, 试件SIWM-2的正向抗弯承载力为1353. 2 kN·m,略低于其他两个试件。端部斜腹杆截面由 H200×150×6×10 减小至 H200×100×6×10时,端部斜腹杆截面较大且未先发生显著破坏,对其抗弯承载力影响很小;当端部斜腹杆采用 H150×100×6×8 截面时,因正向加载斜腹杆受压,致使STMF节点的抗弯承载力略呈降低趋势,但影响不大。

图 17 SIWM系列试件的骨架曲线
4.4 SIWM系列试件的节点转动刚度
图18给出了SIWM系列试件的节点转动刚度退化曲线。可知:SIWM-1、2试件的节点初始转动刚度与BASE试件几乎相等。在SIWM系列试件进入弹塑性阶段后,其节点转动刚度退化趋势基本一致。表明改变桁架斜腹杆截面对STMF连接节点转动刚度影响相对较小。

图 18 SIWM系列试件的节点转动刚度退化曲线
4.5 SIWM系列试件的耗能能力
图19给出了SIWM系列试件的等效黏滞阻尼比。可知,在整个加载过程中,SIWM-1、2试件的等效黏滞阻尼比曲线发展规律与BASE试件的一致,其最大等效黏滞阻尼比为0.3。因此,桁架端斜腹杆在未屈曲的前提下对STMF连接节点的耗能能力影响不明显。

图 19 SIWM 系列试件的等效黏滞阻尼比
5 结 论
本文对STMF连接节点的滞回性能进行了系统分析,重点考察了弦杆截面、桁架高度、端斜腹杆截面等因素的影响,主要得出了以下结论:
1) STMF连接节点的桁架下弦杆应力水平较高,形成全截面屈服或屈曲模式;
2) 随着弦杆截面的增加,STMF连接节点的抗弯承载力、节点初始转动刚度均呈增大趋势;随着弦杆翼缘宽厚比的减小,STMF连接节点的耗能能力呈增加趋势;
3) 随着桁架高度的增加,STMF连接节点的抗弯承载力、节点初始转动刚度均呈增加趋势,其耗能能力略呈增大趋势;
4) 在桁架端部斜腹杆未屈曲前提下,改变端斜腹杆截面对STMF连接节点的力学性能影响不明显。
